معجزة التمييز بين طول المسار والبعد فيما بين السماء والأرض

أ. د. حسين يوسف راشد عمري/ قسم الفيزياء/ جامعة مؤتة - الكرك - الأردنّ

rashed@mutah.edu.jo

د. محمود حسن أبوخرمة / كليّة الهندسة التكنولوجيّة / قسم العلوم الأساسيّة

جامعة البلقاء التطبيقيّة / عمّان - الأردنّ

mah_kharma@hotmail.com

حمزة حسين عمري/ قسم الهندسة الكهربائية

جامعة المسيسيبي -OleMiss / أكسفورد - أمريكا

ملخّص

يقع البحث في أربعة مطالب. يورد المطلبُ الأوّلُ النصوصَ الشرعيّة التي تبيّن البعد بين السماء و الأرض ومسيرة ما بين السماء و الأرض. ويشير إلى أنّ النّصوص الشرعيّة قد فرّقت بين البعد وطول المسيرة . ثمّ يناقش المطلب الثاني بعض أشكال الحركة في مجال جاذبي متماثل المناحي الاتّجاهيّة (isotropic) بهدف بيان أنّ البعد وطول المسير هما شيئان مختلفان: ومن ذلك بيان شكل معادلات لاجرانج (Lagrange) للحركة، وبيان صيغتها عند انعدام قوّة الجاذبيّة، أو عند ثبوتها. وكذلك بيان معادلات الحركة لكوكب حول الشمس, ومسار الرّحلة لوضع قمر صناعي حول الأرض. ثمّ يناقش المطلب الثالث المسار الذي يقابل أقل زمن في حالات: تغيّر قوّة الجاذبيّة، وحالة إهمال قوّة الجاذبيّة، وحالة افتراض ثبوت قوّة الجاذبيّة. ثمّ يناقش المطلب الرابع معادلات الحركة حسب قوانين النسبيّة (Relativity) ومبدأ التغاير (Variational principle) على افتراض أقل زمن للانتقال.

المقدمة

بسم الله والحمد لله وأفضلُ الصّلاة وأتمُّ التّسليم على خير الخلق وأشرف الأنبياء والمرسلين سيدنا محمد وعلى آله وصحبه أجمعين. يُلقي البحثُ ظلالاً على بعض أحاديث الرسول - صلّى اللّه عليه وسلّم - بهدف بيان إعجازها العلمي. فالرسول - صلّى اللّه عليه وسلّم - لا ينطق عن الهوى. وقد أوتي القرآن ومثله معه من السّنة. إنَّ القرآن الكريم والسّنة المطهّرة يشكّلان مصدر هداية البشريّة، ويشيران إلى موضوعات كثيرة في فروع العلم؛ ممّا يؤكد الحاجة إلى جهود أصحاب هذه العلوم حتّى يتعمق إدراكنا وفهمنا للنصوص الشرعيّة.

يقع البحث في مجال الإعجاز العلمي للسنّة المطهرة. وبالتالي فهو ربطٌ غير مسبوق بين حقائق العلم الثابتة وبين أحاديث سيّد المرسلين الّتي فرّقت بين البعد وطول المسير. وليس مجال البحث أن يضيف جديداً في مجال الفيزياء.

المطلب الأوّل: البعد ما بين السماء و الأرض وطول المسيرة

الفرع الأوّل: بعد ما بين السماء و الأرض

جاء في الحديث الذي يرويه العباس بن عبدالمطلب - رضي اللّه عنه - أنّ بعد ما بين السماء والأرض إما واحدة أو اثنتان أو ثلاث وسبعون سنة :.

) – مرّت سحابة على رسول الله صلى الله عليه وسلم فقال هل تدرون ما هذه فقلنا السحاب فقال أو المزن فقالوا أو المزن فقال أو العنان قلنا أو العنان فقال هل تدرون بعد ما بين السماء و الأرض قلنا لا قال إحدى وسبعون أو اثنان وسبعون أو ثلاث وسبعون سنة ...) (الراوي: العباس بن عبد المطلب، خلاصة الدرجة: صحيح، المحدّث: الجورقان ، المصدر: الأباطيل والمناكير، الصفحة أو الر قم1/209 ؛ سنن أبي داود4725-4723 ؛ مسند الإمام أحمد1/206-207 ؛ الترمذي 3320؛ ابن ماجه، 193؛ ضعيف سنن ابن ماجه رقم 34؛ تحقيق د. بشار عواد معروف لسنن ابن ماجه رقم 193؛ وكذلك ضعّفه الألباني).

المزن : السّحاب أو العنان، فكلّها مترادفات.

) - أن رسول الله صلى الله عليه وسلم نظر إلى سحابة فقال : ما تسمون هذه؟ قالوا : السحاب. قال : والمزن ؟ قالوا : والمزن . قال : والعنان ؟ قالوا : نعم . قال : كم ترون بينكم وبين السماء ؟ قالوا : لا ندري . قال : بينكم وبينها إما واحد أو اثنان أو ثلاث وسبعون سنة والسماء فوقها كذلك بينهما مثل ذلك حتى عد سبع سماوات، ... ) (الراوي: العباس بن عبدالمطلب ، خلاصة الدرجة: [حسن] صحيح ، المحدث: ابن القيم، المصدر: اجتماع الجيوش الإسلامية ، الصفحة أو الرقم 87 ).

) - أن رسول الله صلى الله عليه وسلم نظر إلى سحابة فقال : ما تسمون هذه؟ قالوا : السحاب . قال : والمزن ؟ قالوا : والمزن . قال : والعنان ؟ قالوا : نعم . قال : كم ترون بينكم وبين السماء ؟ قالوا : لا ندري . قال : بينكم وبينها إما واحد أو اثنان أو ثلاث وسبعون سنة والسماء فوقها كذلك بينهما مثل ذلك حتى عد سبع سماوات ، ثم فوق السماء السابعة بحر أعلاه وأسفله كما بين سماء إلى سماء ، ثم فوق ذلك ثمانية أوعال بين أظلافهم وركبهم مثل ما بين سماء إلى سماء ، ثم فوق ذلك على ظهورهم العرش ، بين أسفله وأعلاه مثل ما بين سماء إلى سماء ، ثم الله تعالى إلى فوق ذلك) (الراوي: العباس بن عبدالمطلب، خلاصة الدرجة: [حسن] صحيح ، المحدث: ابن القيم ، المصدر: اجتماع الجيوش الإسلامية ، الصفحة أو الرقم 87).

حملة العرش هم ملائكة موكلون بالعرش، وقد يكونون على هيئة أوعال إذا ثبت الحديث.

- (كنت في البطحاء في عصابة فيهم رسول الله صلى الله عليه وسلم فمرت بهم سحابة فنظر إليها فقال ما تسمون هذه قالوا السحاب قال والمزن قالوا والمزن قال والعنان قال أبو داود: لم أتقن العنان جيدا قالوا والعنان ، قال هل تدرون ما بعد ما بين السماء والأرض قالوا لا ندري قال إن بعد ما بينهما إما واحدة أو اثنتان أو ثلاث وسبعون سنة ثم السماء فوقها كذلك حتى عد سبع سماوات ثم فوق السابعة بحر بين أسفله وأعلاه مثل ما بين سماء إلى سماء ثم فوق ذلك ثمانية أوعال بين أظلافهم وركبهم مثل ما بين سماء إلى سماء ثم على ظهورهم العرش ما بين أسفله وأعلاه مثل ما بين سماء إلى سماء ثم الله تبارك وتعالى فوق ذلك ) (خلاصة الدرجة: سكت عنه [وقد قال في رسالته لأهل مكة كل ما سكت عنه فهو صالح[ المحدث: أبو داود - المصدر: سنن أبي داود - الصفحة أو الرقم 4723؛ حسن غريب- المحدث: الترمذي - المصدر: سنن الترمذي - الصفحة أو الرقم3320؛ أشار في المقدمة أنه صح وثبت بالإسناد الثابت الصحيح؛ المحدث: ابن خزيمة ، المصدر: التوحيد، الصفحة أو الرقم235/1؛ فيه يحيى بن العلاء متروك الحديث [ و ] روي من غير طريقه، المحدث: ابن القيسراني ، المصدر: ذخيرة الحفاظ ، الصفحة أو الرقم 4/1868؛ فيه عبد الله بن عميرة قال البخاري لا يعلم له سماع من الأحنف وذكره ابن حبان في الثقات، المحدث: المزي، المصدر: تهذيب الكمال، الصفحة أو الرقم10/391؛ تفرد به سماك عن عبد الله، وعبد الله فيه جهالة، ويحيى بن العلاء متروك الحديث. وقد رواه إبراهيم بن طهمان عن سماك وإبراهيم ثقة. المحدث: الذهبي، المصدر: العلو ، الصفحة أو الرقم 60؛ ضعّفه الألباني المصادر: ضعيف أبي داود، الصفحة أو الرقم 4723؛ ضعيف ابن ماجه ، الصفحة أو الرقم 34؛ ضعيف الترمذي ، الصفحة أو الرقم 3320؛ مشكاة المصابيح ، الصفحة أو الرقم 5659).

الفرع الثاني: مسيرة ما بين السماء و الأرض

(كنفُ الأرضِ مسيرةُ خَمْسِمائةِ عامٍ وبينَ الأرضِ العليا والسَّماءِ الدُّنيا خَمْسُمائةِ عامٍ وبينَ كَنَفِها وكَنَفِها خَمْسُمائةِ عامٍ وما بينَ الأرضِ والعليا والسَّماءِ السَّابعةِ ثُمَّ ما بينَ السَّماءِ السَّابعةِ إلى العرشِ مسيرةُ ذلك كلِّه) (الراوي: أبو ذر الغفاري ، خلاصة الدرجة: رجاله رجال الصحيح إلا أن أبا نصر حميد بن هلال لم يسمع من أبي ذر، المحدث: الهيثمي ، المصدر: مجمع الزوائد ، الصفحة أو الرقم 8/134 ).

20398 - (أن غلظ كل سماء مسيرة خمسمائة عام وما بين كل سماء إلى سماء خمسمائة عام وأنها سبع سماوات وأن الأرض سبع أرضين ) (الراوي:، خلاصة الدرجة: ثابت ، المحدّث: الشوكاني، المصدر: فتح القدير ، الصفحة أو الرقم 1/90 ).

(بينما نبي الله - صلى الله عليه وسلم - جالس وأصحابه إذ أتى عليهم سحاب فقال نبي الله – صلى الله عليه وسلم - هل تدرون ما هذا فقالوا الله ورسوله أعلم قال هذا العنان هذه روايا الأرض يسوقه الله تبارك وتعالى إلى قوم لا يشكرونه ولا يدعونه قال هل تدرون ما فوقكم قالوا الله ورسوله أعلم قال فإنها الرقيع سقف محفوظ وموج مكفوف ثم قال هل تدرون كم بينكم وبينها قالوا الله ورسوله أعلم قال بينكم وبينها مسيرة خمسمائة سنة ثم قال هل تدرون ما فوق ذلك قالوا الله ورسوله أعلم قال فإن فوق ذلك سماءين ما بينهما مسيرة خمسمائة عام حتى عد سبع سماوات ما بين كل سماءين ما بين السماء والأرض ثم قال هل تدرون ما فوق ذلك قالوا الله ورسوله أعلم قال فإن فوق ذلك العرش وبينه وبين السماء بعد ما بين السماءين ثم قال هل تدرون ما الذي تحتكم قالوا الله ورسوله أعلم قال فإنها الأرض ثم قال هل تدرون ما الذي بعد ذلك قالوا الله ورسوله أعلم قال فإن تحتها أرضا أخرى بينهما مسيرة خمسمائة سنة حتى عد سبع أرضين بين كل أرضين مسيرة خمسمائة سنة ... } ) (الراوي: أبو هريرة ، خلاصة الدرجة: من رواية الحسن البصري عن أبي هريرة. منقطع الحسن (عند الحسن البصري) كمتصله صحيح المعاني وكل حرف منه مستند من طرق صحاح، المحدّث: ابن العربي ، المصدر: عارضة الأحوذي ، الصفحة أو الرقم 6/356 ؛ قال عنه الترمذي غريب، 3298؛ أورده ابن الجوزي في العلل المتناهية؛ وضعّفه شعيب الأرناؤوط).

(بينا نحن عند رسول الله صلى الله عليه وسلم إذ مرت سحابة فقال هل تدرون ما هذه قلنا الله ورسوله أعلم قال العنان وروايا الأرض يسوقه الله إلى من لا يشكره من عباده ولا يدعونه أتدرون ما هذه فوقكم قلنا الله ورسوله أعلم قال الرقيع موج مكفوف وسقف محفوظ أتدرون كم بينكم وبينها قلنا الله ورسوله أعلم قال مسيرة خمسمائة عام ثم قال ما الذي فوقها قلنا الله ورسوله أعلم قال سماء أخرى أتدرون كم بينكم وبينها قلنا الله ورسوله أعلم قال مسيرة خمسمائة عام حتى عد سبع سماوات ثم قال هل تدرون ما فوق ذلك قلنا الله ورسوله أعلم قال العرش ثم قال هل تدرون كم بينه وبين السماء السابعة قلنا الله ورسوله أعلم قال مسيرة خمسمائة عام ثم قال [ أتدرون ] ما هذه تحتكم قلنا الله ورسوله أعلم قال أرض تدرون ما تحتها قلنا الله ورسوله أعلم قال أرض أخرى أتدرون كم بينهما قلنا الله ورسوله أعلم قال مسيرة سبعمائة عام حتى عد سبع أرضين ... ) (الراوي: أبو هريرة ، خلاصة الدرجة: فيه الحكم بن عبد الملك وهو ضعيف ، المحدث: الهيثمي ، المصدر: مجمع الزوائد ، الصفحة أو الرقم 7/123، 1/90؛ ضعيف ، المحدث: الألباني ، المصدر: ضعيف الجامع ، الصفحة أو الرقم 6094 ؛ ضعيف ، المحدث: الألباني ، المصدر: ضعيف الترمذي ، الصفحة أو الرقم: 3298 ؛ الراوي: أبو هريرة ، خلاصة الدرجة: غريب من هذا الوجه ، المحدث: الترمذي ، المصدر: سنن الترمذي ، الصفحة أو الرقم 3298 ).

(ثم قال هل تدرون ما الذي تحتكم قالوا الله ورسوله أعلم قال فإنها الأرض). (فإنها الأرض ): الأرضون تقلّ المجرّات (الأرضون السّبع: العمري، 2004) كما تشير إليه الكلمة (أقللن) من الحديث الشريف:) حدثني أن محمدا رسول الله - صلى الله عليه وعلى آله وسلم - لم ير قرية يريد دخولها إلا قال حين يراها : اللهم رب السماوات السبع وما أظللن ، ورب الأرضين السبع وما أقللن ، ورب الشياطين وما أضللن ، ورب الرياح وما ذرين ، فإنا نسألك خير هذه القرية ، وخير أهلها ، ونعوذ بك من شرها ، وشر أهلها وشر ما فيها . وحلف كعب بالذي فلق البحر لموسى ، لأنها كانت دعوات داود حين يرى العدو . ) (الراوي: صهيب بن سنان الرومي القرشي ، خلاصة الدرجة: صحيح ، المحدّث: الوادعي ، المصدر: الصحيح المسند ، الصفحة أو الرقم 509 ).

وفي الحديث الذي يرويه عبدالله بن عمرو بن العاص أنَّ المسيرة من السماء إلى الأرض خمسمائة سنة: (أرسلت من السماء إلى الأرض وهي مسيرة خمسمائة سنة). وفيما يلي بعض متون الحديث:-

روى الترمذي والبغوي وابن القطّان، وأحمد - بسند حسن - أنّ المسيرة من السماء إلى الأرض هي خمسمائة سنة. وفيما يلي روايات الحديث:

- (لو أن رضاضة مثل هذه - وأشار إلى مثل الجمجمة - أرسلت من السماء إلى الأرض هي مسيرة خمسمائة سنة ، لبلغت الأرض قبل الليل ، ولو أنها أرسلت من رأس السلسلة لسارت أربعين خريفا الليل والنهار قبل أن تبلغ أصلها أو قعرها.) (الدرجة: إسناده حسن صحيح - المحدث: الترمذي - المصدر: سنن الترمذي - الصفحة أو الرقم 2588 ).

) - لو أن رضراضة مثل هذه وأشار إلى مثل الجمجمة أرسلت من السماء إلى الأرض وهي مسيرة خمسمائة سنة لبلغت الأرض قبل الليل ، ولو أنها أرسلت من رأس السلسلة لسارت أربعين خريفا الليل والنهار قبل أن تبلغ) (الدرجة: حسن، المحدث: البغوي ، المصدر: شرح السنة ، الصفحة أو الرقم 7/562 ).

) - لو أن رصاصة مثل هذه - وأشار إلى مثل الجمجمة - أرسلت من السماء إلى الأرض ، وهي مسيرة خمسمائة سنة ، لبلغت الأرض قبل الليل ، ولو أنها أرسلت من رأس السلسلة ، لسارت أربعين خريفًا - الليل والنهار - قبل أن تبلغ أصلها أو قعرها.) (الدرجة: حسن ، المحدث: ابن القطان ، المصدر: الوهم والإيهام ، الصفحة أو الرقم 4/374 ).

(لو أن رصاصة مثل هذه وأشار إلى مثل جمجمة أرسلت من السماء إلى الأرض وهي مسيرة خمسمائة سنة لبلغت الأرض قبل الليل ولو أنها أرسلت من رأس السلسلة لسارت أربعين خريفا الليل والنهار قبل أن تبلغ أصلها أو قعرها.) (الدرجة: إسناده صحيح ، المحدث: أحمد شاكر ، المصدر: مسند أحمد ، الصفحة أو الرقم11/80؛ ضعيف ، المحدث: الألباني ، المصدر: ضعيف الجامع ، الصفحة أو الرقم 4805 ؛ ضعيف ، المحدث: الألباني ، المصدر: ضعيف الترمذي ، الصفحة أو الرقم 2588 ).

(لو أن رصاصة مثل هذه وأشار إلى مثل الجمجمة أرسلت من السماء إلى الأرض وهي مسيرة خمسمائة عام لبلغت الأرض قبل الليل ، ولو أنها أرسلت من رأس السلسلة لسارت أربعين خريفا الليل والنهار قبل أن تبلغ أصولها ) (الراوي: عبدالله بن عمرو بن العاص ، خلاصة الدرجة: غريب في رفعه نظر ، المحدث: ابن رجب ، المصدر: التخويف من النار ، الصفحة أو الرقم 132 ؛ رسائل ابن رجب ، الصفحة أو الرقم 4/225 ).

(إن الأرضين بين كل أرض والتي تليها مسيرة خمسمائة عام ، ... ) (الراوي: عبدالله بن عمرو بن العاص ، خلاصة الدرجة: غريب جدا ، المحدث: ابن كثير ، المصدر: تفسير القرآن ، الصفحة أو الرقم: 5/268 ؛ فيه دراج أبو السمح المصري ذكر من جرحه، المحدث: الذهبي ، المصدر: ميزان الاعتدال ، الصفحة أو الرقم 2/25 ؛ إسناده حسن ، المحدث: السيوطي ، المصدر: شرح المواقف ، الصفحة أو الرقم 2 ).

الفرع الثالث : الفرق بين البعد ما بين السماء و الأرض وطول المسيرة بينهما

ذكر العسقلاني في كتابه فتح الباري في شرح صحيح البخاري الحديثين الشّريفين:-

- (هل تدرون ما بعد ما بين السماء والأرض قالوا لا ندري قال إن بعد ما بينهما إما واحدة أو اثنتان أو ثلاث وسبعون سنة).

- (وبين الأرض العليا والسماء الدنيا خمسمائة عام).، (أرسلت من السماء إلى الأرض وهي مسيرة خمسمائة سنة)

ثمّ ذكر أنّ التوفيق بين الحديثين يكون باعتبار بطء المسير أو سرعته (ابن حجر العسقلاني ، فتح الباري شرح صحيح البخاري، كتاب بدء الخلق/ باب 2 / ص 360-361).

وإستدراكاً على ما قاله، فإنَّ البعد ما بين نقطتين وطول المسيرة بينهما يكونان متساويان فقط عندما تكون حركة انتقال الجسم بينهما على خطٍّ مستقيم. وطبقا لقوانين نيوتن في الحركة، فإنّ الجسم يتحرك في خطّ مستقيم فقط عندما تنعدم مركّبة القوة العمودية على المسار. وإنَّ المعادلات المعْلميّة (Parametric equations) للخطّ المستقيم المارّ في النقطة في اتّجاه متّجه الوحدة هي:

, ,

حيث هي المسافة الفاصلة بين النقطتين: ، .

لقد بيّنت الأحاديث السابقة أنّ المسيرة من السماء إلى الأرض هي خمسمائة سنة، بينما ارتفاع السماء على الأرض هو أقلّ من ذلك: (من السماء إلى الأرض وهي مسيرة خمسمائة عام) ، (كم ترون بينكم وبين السماء ؟ قالوا : لا ندري . قال : بينكم وبينها إما واحد أو اثنان أو ثلاث وسبعون سنة). وبالتالي فإنّ الأحاديث المعجزة قد أوضحت وبجلاء أنّ مسير الجسم تحت تأثير قوة الجاذبية الكونيّة لا يكون في خطّ مستقيم، وتؤكده الآية الكريمة : (يُدَبِّرُ الْأَمْرَ مِنَ السَّمَاءِ إِلَى الْأَرْضِ ثُمَّ يَعْرُجُ إِلَيْهِ فِي يَوْمٍ كَانَ مِقْدَارُهُ أَلْفَ سَنَةٍ مِمَّا تَعُدُّونَ) (السجدة آية 5). وبالتالي فإنّ طول المسير بين السماء والأرض يعدل حوالي سبعة أمثال البعد بينهما.

الفرع الرابع: شفير جهنم

بيّنت الأحاديث الشريفة أنَّ الحجر يلقى من شفير (شفة) جهنم ، فيهوي فيها سبعين عاما ًلا يدرك لها قعر:-

خطبنا عتبة بن غزوان . فحمد الله وأثنى عليه ثم قال : أما بعد . فإن الدنيا قد آذنت بصرم وولت حذاء . ولم يبقى منها إلا صبابة كصبابة الإناء . يتصابها صاحبها . وإنكم منتقلون منها إلى دار لا زوال لها . فانتقلوا بخير ما بحضرتكم . فإنه قد ذكر لنا أن الحجر يلقى من شفة جهنم . فيهوي فيها سبعين عاما ًلا يدرك لها قعر . و والله ! لتملأن . أفعجبتم ؟ ولقد ذكر لنا أن ما بين مصراعين من مصاريع الجنة مسيرة أربعين سنة . وليأتين عليها يوم وهو كظيظ من الزحام . ولقد رأيتني سابع سبعة مع رسول الله صلى الله عليه وسلم . ما لنا طعام إلا ورق الشجر . حتى تقرحت أشداقنا . فالتقطت بردة فشققتها بيني وبين سعد بن مالك . فاتزرت بنصفها واتزر سعد بنصفها . فما أصبح اليوم منا أحد إلا أصبح أميرا على مصر من الأمصار. وإني أعوذ بالله أن أكون في نفسي عظيما وعند الله صغيرا . وإنها لم تكن نبوة قط إلا تناسخت ، حتى يكون آخر عاقبتها ملكا . فستخْبُرون وتجربُون الأمراء بعدنا . ) (الراوي: خالد بن عمير العدوي ، خلاصة الدرجة: صحيح ، المحدث: مسلم ، المصدر: المسند الصحيح ، الصفحة أو الرقم 2967 ).

بصرم: انقطاع.

(إن الصخرة العظيمة لتلقى من شفير جهنم فتهوي فيها سبعين عاما ًما تفضي إلى قرارها) (الراوي: عتبة بن غزوان، خلاصة الدرجة: صحيح، المحدث: الألباني، المصدر: صحيح الترمذي ، الصفحة أو الرقم 2575؛ صحيح الجامع ، الصفحة أو الرقم 1662 ).

(لو أن حجرا مثل سبع خلفات، ألقي عن شفير جهنم هوى فيها سبعين خريفا لا يبلغ قعرها ) (الراوي: أنس بن مالك و معاذ بن جبل و أبو أمامة الباهلي و أبو هريرة، خلاصة الدرجة: صحيح ، المحدث: الألباني، المصدر: صحيح الجامع، الصفحة أو الرقم5248 ).

خلفات: نياق.

ليس من السّهل استخدام العبارة (سبعين عاما ًلا يدرك لها قعر) لمعرفة نصف قطر جهنّم، وذلك لعوامل كثيرة منها:

- هنا يوجد قوة الإشعاع الجهنّمي (إذا رأتهم من مكان بعيد سمعوا لها تغيّظاً وزفيراً) المؤثرة في عكس اتّجاه جاذبيّة جهنّم. وهذه غير مؤثرة في حالة المسير من السماء إلى الأرض العليا التي تحمل مجرّتنا. ويوجد كذلك قوى كهرومغناطيسية؛ حيث المادة في حالة البلازما. كما وتؤثر قوى الضغط واللزوجة. هذا ولا يمكن معرفة الصيغ الملائمة لأيٍّ من هذه القوى.

- لا يعرف ما إذا كانت جهنّم عبارة عن ثقب أسود أو خلاف ذلك، بل هي عالم غيبي.

- هنا العبارة: (ألقي عن شفير جهنم)، بينما في أحاديث المسير بين السّماء والأرض وردت العبارة (أرسلت من السماء إلى الأرض). وقد يكون الإرسال برفقة الملك، بينما الإلقاء لا يكون برفقة الملك. وهذا يزيد في صعوبة معرفة النسبة بين شفير جهنم إلى ارتفاع السماء عن الأرض.

المطلب الثاني: معادلة الحركة في مجال جاذبي متماثل المناحي الإتجاهيّة (isotropic)

الفرع الأوّل: معادلات لاجرانج للحركة في حالة التماثل الكروي (spherical symmetry)

في محاور الإسناد الكرويّة تكتب صيغة مربّع سرعة جسم على النّحو:

إذا تحرّك الجسم الذي كتلته قريباً من حافّة البناء السماوي الأوّل (والّذي هو قشرة كرويّة) تحت تأثير قوة جاذبيّة كتلة المادة الكونيّة (تساوي تقريبا الكتلة الموجودة داخل البناء السماوي الأوّل)، فإنّ دالّة لاجرانج (Lagrangian) تكتب على النّحو الآتي:

حيث طاقة الجسم الحركيّة (Kinetic energy)، و طاقة وضعه (Potential energy) في المجال الجاذبي لكتلة المادة الكونيّة . عند قسمة دالة لاجرانج على كتلة الجسم نحصل على العلاقة:

باستخدام معادلة أويلر- لاجرانج (Euler-Lagrange) يمكننا كتابة مركبات معادلة الحركة على النحو الآتي:

صيغة مركبة المعادلة في البعد الزاوي هي:

(2-1)

صيغة مركبة معادلة الحركة في البعد هي:

(2-2)

صيغة مركبة معادلة الحركة في البعد الزاوي هي:

حيث ثابت.

(2-3)

وكما هو واضح، فإنّ المعادلات السّابقة للحركة {(2-3), (2-2),(2-1)} ليست معادلات حركة في خط مستقيم.

الفرع الثاني: شكل معادلات الحركة عند انعدام الجاذبيّة

وأمّا في الحالة التي تكون فيها الكتلة ، فيمكن كتابة مركّبات التّسارع من معادلات الحركة (2-1) - (2-3) على النحو الآتي:

(2-4)

(2-5)

(2-6)

حيث ثابت. إذن تسارع الجسم يساوي صفراً، وبالتالي فهو يتحرّك بسرعة ثابتة:

(2-7)

(2-8)

حيث متجه وحدة شعاعي (radial) ، متجه وحدة باتّجاه زيادة الزّاوية ، و متجه وحدة باتّجاه زيادة الزّاوية .

الفرع الثالث: معادلات الحركة على افتراض ثبوت قوّة الجاذبيّة

ورد في الحديث الذي يرويه عبدالله بن عمرو بن العاص: (إن الأرضين بين كل أرض والتي تليها مسيرة خمسمائة عام). ولقد روى كلٌّ من خالد بن عمير العدوي؛ وعتبة بن غزوان؛ وأنس بن مالك؛ ومعاذ بن جبل؛ وأبو أمامة الباهلي وأبو هريرة أن الحجر يلقى من شفة جهنم, فيهوي فيها سبعين عاما ًلا يدرك لها قعر. وبالتالي فإنّ البعد بين السماء الأولى والأرض العليا يكون قليلا مقارنة مع قعر جهنّم ، والذي هو الآخر قليل بالمقارنة مع نصف قطر السماء الأولى.

لذا من أجل تبسيط المسألة، فإنّه يمكننا التعامل مع قوّة الجاذبية على أنّها ثابتة عند الانتقال بين السماء الأولى والأرض العليا. وفي هذه الحالة تكون قوة الجاذبيّة تقريباً ، حيث يمثّل نصف قطر السماء الدنيا، و كتلة المادّة الكونيّة داخل البناء السّماوي الأوّل، وتمثّل كتلة الجسم المتحرّك. و هي التّسارع الثابت خلال هذا الانتقال. وبالتالي يمكن كتابة دالة لاجرانج (Lagrangian) على الصّورة:

معادلتا أويلر لاجرانج (Euler-Lagrange) لمركبتي معادلة الحركة في البعدين الزاوييّن هما:

وتعطيا نفس المعادلتين (2-1,2-3) اللتين تمّ الحصول عليهما عند السماح بتغيّر قوّة الجاذبيّة:

(2-9)

(2-10)

معادلة أويلر لاجرانج لمركبة معادلة الحركة في البعد القطري هي:

وعند التّعويض عن دالّة لاجرانج نحصل على المركّبة القطريّة للتسارع:

(2-11)

وهي كما ترى ليست معادلات حركة في خط مستقيم. وبالتالي هنالك فرق بين طول المسير والبعد الّذي هو خطّ مستقيم خلافاً لمسار الجسم الّذي لا يكون مستقيما إلاّ عند انعدام القوّة المؤثّرة.

الفرع الرابع: معادلة الحركة لكوكب حول الشمس.

Energy equation of an obrit in a central field

معادلة حفظ الطاقة في مجال جاذبي مركزي هي:

طاقة وضع الجاذبية لنظام ثنائي تتناسب طرديّاً مع حاصل ضرب الكتلتين ، وعكسيّاً مع المسافة الفاصلة بين مركزي ثقليهما:

وبدلالة المتغيّر ، يمكننا إعادة كتابة المعادلة على النحو الآتي:

هنا الثابت عبارة عن الزخم الزاوي لكل وحدة كتلة (angular momentum per unit mass).

وبالتالي يمكن كتابة معادلة حفظ الطاقة على النحو:

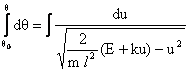
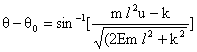
عند تعويض القيم : و ، يصبح الحلّ على الصيغة التالية:

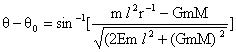
عندما نختار قيمة ثابت التكامل ، يصبح الحلّ على الشكل التالي:

حيث التغاير المركزي للمسار (the eccentricity of the orbit) هو:

يتحدّد المسار تبعاً للطاقة الميكانيكيّة (وبالتالي تبعاً للتغاير المركزي ) على النحو الآتي (الشكل الآتي):

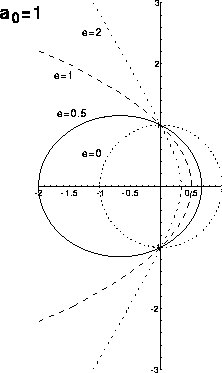
- قطع ناقص (Ellipse): ؛

- قطع مكافئ :( Parabola) ؛

- قطع زائد Hyperbola)) : .

هذه هي المسارات المحتملة في المستوى القطبي . وبالتالي يتّضح لنا أنّ البعد المستقيم بين نقطتين لا يساوي طول المسار الذي يسلكه جسم عند انتقاله بين هاتين النّقطتين.

Hohmann minimum-energy trajectory

The minimum-energy transfer between circular orbits is an elliptical trajectory called the Hohmann trajectory (following two figures). It is shown below for the Earth-Mars case, where the minimum total delta-v expended is 5.6 km/s. The values of the energy per unit mass on the circular orbit and Hohmann trajectory are shown, along with the velocities at perihelion (closest to Sun) and aphelion (farthest from Sun) on the Hohmann trajectory and the circular velocity in Earth or Mars orbit. The differences between these velocities are the required delta-v values in the rocket equation.

Kepler's third law, T² = const x a³, can be used to calculate the time required to traverse a Hohmann trajectory by raising to the 3/2 power the ratio of the semimajor axis of the elliptical Hohmann orbit to the circular radius of the Earth's orbit and dividing by two for one-way travel. For example, calling the travel time for an Earth-Mars trip T and the semimajor axis of the Hohmann ellipse a,

a = (1 AU + 1.5 AU)/2 = 1.25 AU

T = 0.5 (a / 1 AU)^3/2 years = 0.7 years = about 8.4 months

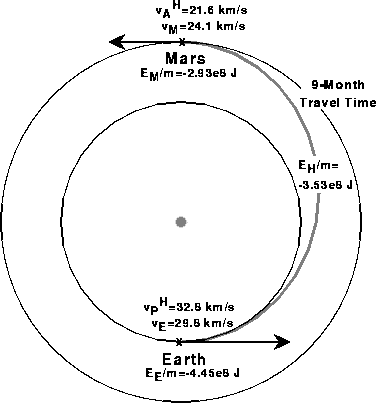
Trajectory from Earth to Mars.

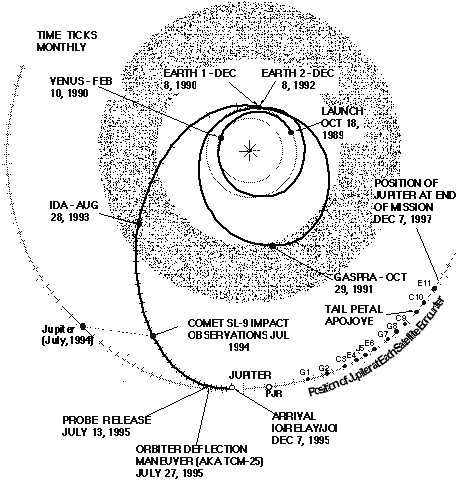
Trajectory from Earth to Jupiter.

الفرع الخامس: مسار الرحلة لوضع قمر صناعي حول الأرض

يبيّن الشكل (1) مسار الرّحلة لوضع قمر صناعي حول الأرض (Thomson, 1961, P. 249).

إنّ طول المسار الذي يرافق دفع الصاروخ يكون صغيراً بالمقارنة مع نصف قطر الأرض . وبالتالي يمكننا افتراض ثبوت قوّة الجاذبيّة. تمثل التسارع الثابت أثناء دفع الصاروخ. وبالتالي يمكن كتابة معادلات الحركة على النحو الآتي (Thomson, 1961, PP. 248-252):

(3-1)

(3-2)

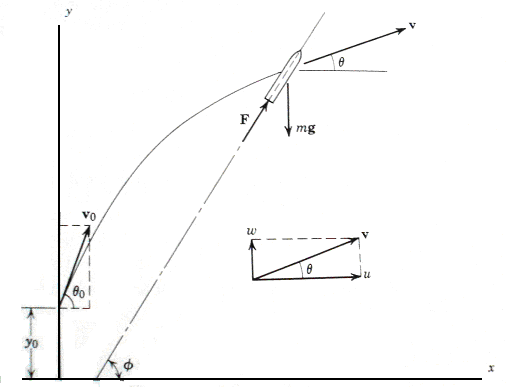
شكل رقم (1): يبيّن الشكل مسار الرحلة لوضع قمر صناعي حول الأرض. المسار يمثله المنحنى المتّصل، فهو ليس خطّ مستقيم.

(3-3)

إنّ تكامل العلاقة (3-1) على زمن دفع الصّاروخ () يعطي:

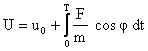(3-4)

المطلوب أن تكون قيمة أكبر ما يمكن عندما تصبح المركّبة الرّأسية للسرعة . وأن يتحقّق في نفس الوقت قيدا العلاقتين: (3-2) ، (3-3).

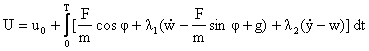(3-5)

المطلوب أن تكون قيمة في العلاقة (3-5) أكبر ما يمكن عندما تتحقّق الشّروط الحدّيّة الآتية:

, , ,

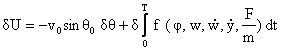(3-6)

حيث

وهذا يعطي المعادلات الآتية:

, ,

, ,

, ,

وهذا يعطي في النهاية المعادلة الآتية (وللتفصيل أنظر: Thomson, 1961, PP. 251-252):

المطلب الثالث: المسار الذي يقابل أقل زمن

الفرع الأوّل: معادلات المسار حالة تغيّر قوّة الجاذبيّة

عنصر الطول للمسار يعطى بالعلاقة التالية:

يمكن كتابة معادلة حفظ الطاقة على النحو

يمكن كتابة عنصر الزمن على النحو:

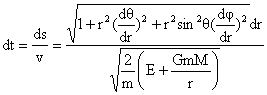
يمكن كتابة التكامل الذي يعطي الزمن على الشكل

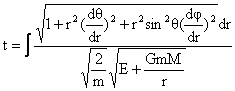
(3-1)

المسار الذي يقابل أقلّ زمن، يجب أن يحقّق المعادلتين التاليتين:

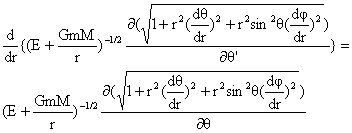
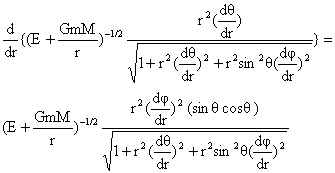} (3-2)

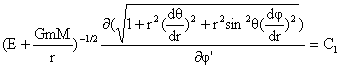
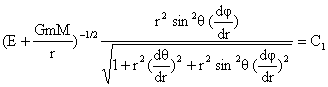(3-3)

ومن الواضح أنّ المعادلتين معقّدتان، ليس حلّهما سهلاً. فالجسم يتحرّك في الأبعاد الثلاثة .

الفرع الثاني: معادلات المسار حالة إهمال قوّة الجاذبيّة

وعند انعدام الجاذبية، ، تصبح المعادلتان (3-2) و (3-3) على الشكل:

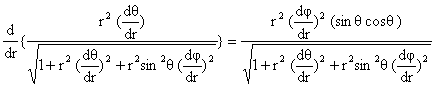(3-4)

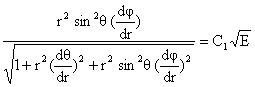(3-5)

الفرع الثالث: معادلات المسار على افتراض ثبوت قوّة الجاذبيّة

بيّنت الأحاديث أنّ البعد بين السماء الأولى والأرض العليا يكون قليلاً مقارنة مع نصف قطر السماء الأولى. لذا من أجل تبسيط المسألة، يمكننا التعامل مع قوّة الجاذبية على أنّها ثابتة عند الانتقال بين السماء الأولى والأرض العليا. وفي هذه الحالة تكون قوة الجاذبيّة تقريباً ، حيث يمثّل الثابت نصف قطر السّماء الدّنيا ، ويمثّل الثابت كتلة المادّة الكونيّة داخل البناء السّماوي الأوّل، وتمثّل كتلة الجسم المتحرّك. وبالتالي عند استخدام العلاقة (3-1)، يمكن كتابة على النّحو الآتي:

المسار الذي يقابل أقلّ زمن يجب أن يحقّق المعادلتين التاليتين:

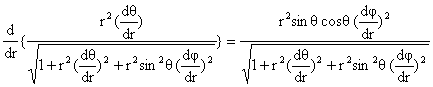(3-6)

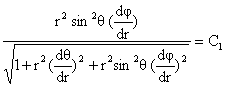(3-7)

المطلب الرابع: النسبيّة العامّة (General Relativity)

المسافة الحقيقيّة (proper distance) بين نقطتين و على خطّ قطري (radial line) هي:

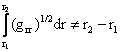
من النتائج المهمّة لقوانين نيوتن في الجاذبيّة أنّ المجال الجاذبي (gravitational field) لكتلة ذات تماثل كروي (spherical symmetry) عند نقطة يعتمد على الكتلة المتواجدة داخل السطح الكرويّ المارّ بالنقطة (كما الحال في قانون جاوس في الكهرباء). المجال خارج الكتلة لا يعتمد على الزّمن (constant in time): .

وهذه النتيجة صحيحة في النسبيّة العامّة (general relativity)، وهي عبارة عن نظريّة تعرف بـ (Birkhoff's theorem): وتنصّ على الآتي:

The only vacuum, spherically symmetric gravitational field is static. It is called Schwarzschild metric:

الكلمة فراغ (vacuum): تشير إلى منطقة في الزّمكان (spacetime) حيث التأثير الجاذبي (gravitational effect) لأيّ مادّة موجودة هو مهمل (Shapiro pp. 123-124).

يتّضح أنّ عنصر الطول (metric) يعتمد على كلّ من الكتلة ، والزمن ، إضافة إلى اعتماده على الإحداثيات .

الفرع الأوّل: قوى الجاذبيّة

معادلة حركة جسيم يتأثير بقوّة الجاذبيّة فقط هي (Weinberg, p. 71):

(4-1)

حيث تدعى (affine connection) وتعريفها هو:

يمكن الحصول على معادلة الحركة هذه من مبدأ التغاير. المعْلمة (المؤشّر) الاعتباطي (arbitrary parameter) يصف المسار. الزّمن اللازم لانتقال الجسم من النقطة إلى النقطة هو (Weinberg, p. 76):

حيث عبارة عن metric tensor ، وتعريفه هو (Weinberg, p. 71):

عند تغيير المسار مع تثبيت الأطراف ( عند كلّ من و )، فإنّ التغيّر في هو (Weinberg, p. 77):

(4-2)

وبالتالي فإنّ مسار الزّمكان (space-time) الذي يحقّق معادلة الحركة (4-1) يجعل زمن الانتقال أقل ما يمكن. ومعادلة الحركة ليست معادلة خطّ مستقيم.

الخلاصة

تبيّن أنّ النّصوص الشرعيّة قد فرّقت بين البعد وطول المسيرة. وناقش البحث بعض أشكال الحركة في مجال جاذبي متماثل المناحي الاتّجاهيّة بهدف بيان أنّ البعد وطول المسير هما شيئان مختلفان طبقاً للنّصوص الشرعيّة. أوضحت معادلات لاجرانج لأشكال الحركة التي ناقشها البحث أنّ المسار بين نقطتين هو أطول من البعد الفاصل بينهما. وهذا ما أكّده مبدأ التغاير على افتراض أقل زمن للانتقال. وبالتالي يتّضح الإعجاز العلمي في أحاديث الرسول الّتي أوضحت وبجلاء أنّ طول المسير بين السّماء والأرض (خمسمائة سنة) هو تقريباً سبعة أضعاف المسافة الفاصلة بينهما (إما واحد أو اثنان أو ثلاث وسبعون سنة). وهذا دليل قاطع أنّ كلام الرسول - صلّى اللّه عليه وسلّم - وحيّ من اللّه ربّ العالمين ومودع القوانين التي تحكم الكون والخلق أجمعين.

المصادر

1) القرآن الكريم

2) كتب السّنّة المطهّرة

3) ابن حجر العسقلاني، أحمد بن علي (773-852 هـ) ، فتح الباري شرح صحيح البخاري، دار الكتب العلمية- بيروت / الطبعة الثالثة (1997 م - 1418 هـ) كتاب بدء الخلق/ باب 2 / ص 360-361

المراجع العربيّة

1) العمري، حسين يوسف راشد، الأرضون السّبع لغز المادّة المظلمة وبوّابة تكميم الكون، مجلّة كليّة المعارف الجامعة، الأنبار، (2004)، العدد السادس، ص 10.

المراجع الأجنبيّة:

1) Shapiro, S., and Teukolsky, S. Black Holesm White Dwarfs, and Neutron Stars. The physics of compact objects. 1983 John Wiley (New York), pp. 123-124.

2) Thomson, W. T., Introduction to space dynamics, 1961 John Wiley (New York), PP. 248-252.

3) Weinberg, Steven. Gravitation and cosmology: Principles and applications of the general theory of relativity. 1972 John wiley and sons New York.