بعض جوانب الإعجاز الرياضياتي في آية خلق الأزواج

أ. د. حسين يوسف راشد عمري

قسم الفيزياء/ جامعة مؤتة/ الأردن

rashed@mutah.edu.jo

د. تسنيم حسين يوسف عمري

قسم الهندسة الكهربائية/ الجامعة الهاشمية/ الأردن

ملخّص

وكلّ شيئين أو مخلوقين اقترن أحدهما بالآخر هما زوجان أو ضدّان كالذّكر والأنثى. والزّوج كذلك هو الصّنف من كلّ شيء. فالمخلوقات كلّها أضداد وأصناف. نظام الزّوجيّة في الخلق يشمل الأحياء والجمادات. ويشمل كلّ المخلوقات، والآية قالت: (ومن كلّ شيء خلقنا زوجين). يركّز البحث على بيان أشكال الأزواج الرياضيّة من عمليات حسابيّة واقترانات ودوال خاصّة وانتقالات، من أجل توضيح الإعجاز الرياضي في الآية الكريمة.

Abstract

Every two things or two creatures having a joint relationship are pairs or opposite; like male and female. A pair is also a kind of something. Allah created in pairs all things. Pairing system includes both living and nonliving things as well. It includes all creatures. Of every thing Allah has created pairs. This article presents various mathematical pairs, arithmetic operations, functions, special functions and transformations in order to clarify this miraculous Verse.

المقدِّمة

ملاحظة: هنا التقديم شبيه بما ورد في بحث الأزواج الفيزيائيّة. لذا يمكن الإنتقال مباشرة إلى المطلب الثاني ( بعض الأزواج في الرياضيات).

الزّوج في اللّغة خلاف الفرد ... قال أبو بكر: العرب لا يتكلّمون بالزّوج موحّداً مثل قولهم زوج حمام، ولكنّهم يثنونه فيقولون: عندي زوجان من الحمام، يعنون ذكراً وأنثى، وعندي زوجان من الخفاف يعنون اليمين والشمال، ويوقعون الزوجين على الجنسين المختلفين نحو الأسود والأبيض والحلو والحامض. قال ابن سيدة: ويدلّ على أنّ الزوجين في كلام العرب اثنان قول الله عز وجل: (وَأَنَّهُ خَلَقَ الزَّوْجَيْنِ الذَّكَرَ وَالْأُنْثَى) [النجم 45] (ابن منظور 1993 ج 6 ص 107-109). قال الله تعالى –مخاطباً نوح عليه السّلام-: (فَاسْلُكْ فِيهَا مِنْ كُلٍّ زَوْجَيْنِ اثْنَيْنِ) [المؤمنون 27]. وكان الحسن يقول في قوله عزّ وجل: (وَمِنْ كُلِّ شَيْءٍ خَلَقْنَا زَوْجَيْنِ لَعَلَّكُمْ تَذَكَّرُونَ) [الذّاريات 49]؛ قال: السّماء زوج، والأرض زوج، والشتاء زوج، والصيف زوج، والليل زوج، والنهار زوج (العمادي 1994 ج 8 ص 143).

والأصل في الزوج الصّنف والنوع من كلّ شيء. وكلّ شيئين مقترنين، شكلين كانا أو نقيضين، فهما زوجان؛ وكلّ واحد منهما زوج. وعن ابن سيدة: الرّجل زوج المرأة وبعلها، وهي زوجه وزوجته وامرأته ... وجمعُ الزّوج أزواج وزِوجَةٌ، قال الله تعالى: (يَا أَيُّهَا النَّبِيُّ قُلْ لِأَزْوَاجِكَ) [الأحزاب 28]. وقال الله تعالى: (وَزَوَّجْنَاهُم بِحُورٍ عِينٍ) [الدخان 54] أي قرناهم بهنّ، وقوله تعالى: (احْشُرُوا الَّذِينَ ظَلَمُوا وَأَزْوَاجَهُمْ) [الصافات 22] معناها: ونظراءهم وضرباءهم وقرناءهم وأمثالهم (ابن منظور 1993 ج 6 ص 107-109).

وتزاوج القوم وازدوجوا: تزوّج بعضهم بعضا ... وازدوج الكلام وتزاوج: أشبه بعضُه بعضاً في السّجع أو الوزن، أو كان لإحدى القضيّتين تعلّق بالأخرى. وزوّج الشيء بالشيء، وزوّجه إليه: قرنه ... وكذلك الزّوج المرأة، والزّوج المرء، قد تناسبا بعقد النكاح. وقوله تعالى: (أَوْ يُزَوِّجُهُمْ ذُكْرَانًا وَإِنَاثًا وَيَجْعَلُ مَنْ يَشَاءُ عَقِيمًا) [الشورى 50] قال الفراء: يجعل بعضهم بنين وبعضهم بنات، فذلك التّزويج. قال أبو منصور: أراد بالتّزويج التّصنيف؛ والزّوج: الصّنفُ. والذّكر صنف، والأنثى صنف ... والزّوج: الصّنف من كلّ شيء. وفي التنـزيل: (وَتَرَى الْأَرْضَ هَامِدَةً فَإِذَا أَنْـزَلْنَا عَلَيْهَا الْمَاءَ اهْتَزَّتْ وَرَبَتْ وَأَنْبَتَتْ مِنْ كُلِّ زَوْجٍ) [الحج 5] قيل: من كلّ لون أو ضرب حسن من النبات (ابن منظور 1993 ج 6 ص 107-109).

وقوله تعالى: (وَآخَرُ مِنْ شَكْلِهِ أَزْوَاجٌ) [ص 58] قال: معناه ألوان وأنواع من العذاب، ووصفه بالأزواج، لأنّه عنى به الأنواع من العذاب والأصناف منه (ابن منظور 1993 ج 6 ص 107-109).

بعض أزواج اللغة

إسلام كفر، جنّة نار، آخرة دنيا، طهر نجاسة، بيع شراء، مدين دائن، زواج طلاق، إمساك تسريح، مقدّم مؤخّر، ذكر أنثى، غنى فقر، كرم بخل، شجاعة جبن، مرتفع منخفض، جبل وادي، طول قصر، ذكاء غباء، حسنة سيّئة، أجر وزر، بصيرة عمى، حلم غضب، إيثار أنانيّة، إصلاح إفساد، سهل حزن، علوّ سفول، بروز ضمور، مصقول خشن، فرح ترح، سعادة شقاوة، نظافة قذارة، جديد قديم، كثير قليل، كبير صغير، حضور غياب، جميل قبيح، ظاهر باطن، قدوم مغادرة، يغدو يروح، خماص بطان، ظِلّ حرور، مناصرة عداء، سلم حرب، نجاح فشل، فلاح خيبة، اجتهاد كسل، غطاء فراش، أظلّ أقلّ، وعي غفلة، يقين جهل.

المطلب الأوّل: الخلق أزواج

الآيات الّتي بيّنت أنّ الخلق أزواج هي:

(سُبْحَانَ الَّذِي خَلَقَ الْأَزْوَاجَ كُلَّهَا مِمَّا تُنْبِتُ الْأَرْضُ وَمِنْ أَنْفُسِهِمْ وَمِمَّا لَا يَعْلَمُونَ) [يس 36]

(والَّذِي خَلَقَ الْأَزْوَاجَ كُلَّهَا) [الزّخرف 12]

(وَمِنْ كُلِّ شَيْءٍ خَلَقْنَا زَوْجَيْنِ لَعَلَّكُمْ تَذَكَّرُونَ) [الذّاريات 49].

الفرع الأوّل: بعض أصناف وأزواج الخلق التي أشار لها المفسّرون

أخرج ابن المنذر عن ابن جرير في تفسير قوله تعالى: (سُبْحَانَ الَّذِي خَلَقَ الْأَزْوَاجَ كُلَّهَا) [يس 36]: الأصناف كلّها. الملائكة زوج، والإنس زوج، والجنّ زوج، ومما تنبت الأرض زوج، وكل صنف من الطير زوج، ثم فسر فقال: (مِمَّا تُنْبِتُ الْأَرْضُ وَمِنْ أَنْفُسِهِمْ وَمِمَّا لَا يَعْلَمُونَ) [يس 36] الروح لا يعلمه الملائكة ولا خلق الله، ولم يطلع على الرّوح أحد (السيوطي م7، ص 55).

وأوضحَ حديثُ الرّوحِ أنّ روح المؤمن روحٌ طيّبة تخرج بأطيب رائحة، ويقابلها روح الكافر؛ إذ هي خبيثة تخرج ولها أنتن ريح جيفة. وقد بيّن القرآن أزواجَ النّفس: (وَنَفْسٍ وَمَا سَوَّاهَا * فَأَلْهَمَهَا فُجُورَهَا وَتَقْوَاهَا * قَدْ أَفْلَحَ مَنْ زَكَّاهَا * وَقَدْ خَابَ مَنْ دَسَّاهَا) [الشمس 7-10]، وأقسم سبحانه بالنّفس اللّوامة (وَلَا أُقْسِمُ بِالنَّفْسِ اللَّوَّامَةِ) [القيامة 2].

الملائكة أصناف ولهم مهام ووظائف مختلفة. جبريل –عليه السّلام- هو الملك الموكلُ بالوحي، وهناك ملائكةُ العذاب، والرّحمة، وملك النّار والجنّة، والملائكة الموكلة بتصريف الرّياح والسّحاب، والجبال، وملك الموت، والملائكة الّتي تنفخ الرّوح في الجنين، والحفظة، والكتبة، وهناك حملة العرش. وللملائكة أعداد مختلفة من الأجنحة (جَاعِلِ الْمَلَائِكَةِ رُسُلًا أُولِي أَجْنِحَةٍ مَثْنَى وَثُلَاثَ وَرُبَاعَ يَزِيدُ فِي الْخَلْقِ مَا يَشَاءُ) [فاطر 1].

وقوله (والَّذِي خَلَقَ الْأَزْوَاجَ كُلَّهَا) [الزّخرف 12] أي: والّذي خلق كلّ شيء فزوّجه (الطبري م 13 ج 25 ص 68). و (الْأَزْوَاجَ) الأجناس والأصناف (الزّمخشري19 م 3 ص 479، 322). أي أنواع وأصناف المخلوقات من كلّ شيء (أبو حيّان 1992 ج 9 ص 361، الرّازي 1995 م 14 ج 27 ص 198). وعن ابن عباس الأزواج الضروب والأنواع كالحلو والحامض والأبيض والأسود والذكر والأنثى. وعن الحسن: السّماء والأرض، والليل والنهار، والشمس والقمر، والبرّ والبحر، والموت والحياة، فعدّد أشياء، وقال: كلّ اثنين منها زوجين (الزّمخشري 19 م 4 ص 20، أبو حيّان 1992 ج 9 ص 560، العمادي 1994 ج 8 ص 143). قال مجاهد: إشارة إلى المتضادات والمتقابلات، كالليل والنهار، والشقاوة والسعادة، والهدى والضلال، والسّماء والأرض، والسواد والبياض، والصحة والمرض، والكفر والإيمان (الطبري م 13 ج 27 ص 12-13). إنَّ الله تبارك وتعالى، خلق لكلّ ما خلق من خلقه ثانياً له مخالفاً في معناه، فكلّ واحد منهما زوج للآخر، ولذلك قيل: خلقنا زوجين. فهو أدل على القدرة التي توجد الضّدين (أبو حيّان 1992 ج 9 ص 560). قال المنطقيّون المراد بالشيء الجنس وأقلّ ما يكون تحت الجنس نوعان فمن كلّ جنس أو زوج خلق نوعين: من الجوهر مثلا المادّي والمجرّد، ومن المادّي النامي والجامد، ومن النامي المدرك والنبات، ومن المدرك الناطق والصامت، وكلّ ذلك يدلّ على أنّه سبحانه فردٌ لا كثرة فيه (الرّازي 1995 م 14 ج 28 ص 228، أبو حيّان 1992 ج 9 ص 560، العمادي 1994 ج 8 ص 143). وقال بعض المحقّقين كلّ ما سوى الله فهو زوج كالفوق والتحت واليمين واليسار والقدّام والخلف والماضي والمستقبل والصيف والشتاء والربيع والخريف (أبو حيّان 1992 ج 9 ص 361، الرّازي 1995 م 14 ج 27 ص 198، العمادي 1994 ج 8 ص 41). وكونها أزواجاً يدلّ على كونها محدثة مسبوقة بالعدم، فأمّا الحقّ سبحانه فهو فرد مطلقٌ منـزّه عن الضّدّ والنّدّ والمقابل والمعاضد والمعارض، هو الفرد الذي يقدر على خلق الشيء وخلافه، وابتداع زوجين من كلّ شيءٍ (أبو حيّان 1992 ج 9 ص 361، الرّازي 1995 م 14 ج 27 ص 198، أبو حيّان 1992 ج 9 ص 560، الزّمخشري 19 م 4 ص 20، الطبري م 13 ج 27 ص 12-13).

الفرع الثاني: المخلوقات كلّها أزواج

(سُبْحَانَ الَّذِي خَلَقَ الْأَزْوَاجَ كُلَّهَا مِمَّا تُنْبِتُ الْأَرْضُ وَمِنْ أَنْفُسِهِمْ وَمِمَّا لَا يَعْلَمُونَ) [يس 36] هذه الآية من معجزات القرآن الكثيرة، إذ تتحدّث عن معنى يستحيل على أحد من البشر أن يتكلّم فيه ساعة نـزول هذا القرآن، مما يدل دلالة قطعيّة على أنَّ هذا القرآن من عند الله عز وجل (حوّى 19 م 8 ص 4650 ). والأزواج هي الشّيء ومقابله، كما في عالم المعاني كالصدق والكذب، والحقّ والباطل، والإيمان والكفر، والضلال والهدى (الرّازي 1995 م 14 ج 28 ص 228، الخطيب 1970 م 12 ص 931). وإنَّ المخلوقات كلَّها من أزواج، هي الذّكر والأنثى كما في عالم الأحياء من حيوان (أبو حيّان 1992 ج 9 ص 560)، وممّا تنبت الأرض من سائر الأصناف من نبات و زروع وثمار وأزاهير وغير ذلك على اختلاف أجناسها (الخطيب 1970 م 12 ص 931، ابن كثير 1994م 3 ص 753، حوّى 19 م 9 ص 5126، الزّمخشري 19 م 4 ص 20). وخلق الله الأحياء أزواجاً؛ النبات فيها كالإنسان. ومثل ذلك غيرهما (قطب 1996 م 5 ص2967 ). وقوله تعالى: (خَلَقَ الْأَزْوَاجَ) أي الأنواع المتشاكلة المتباينة في الأوصاف وفي الطعوم والأرايح والأشكال والهيئات والطبائع وغير ذلك من أمور لا يحصيها إلاّ الله تدلّ أعظم دلالة على كمال القدرة وعظيم الحكمة والاختيار في الإرادة، وأكّد بقوله: (كُلَّهَا) لإفادة التّعميم، ثمّ زاد الأمر تصريحاً بالبيان بقوله: (مِمَّا تُنْبِتُ الْأَرْضُ) فدخل فيه الحيوان والجماد وكلّ نجم وشجر وغيره من كلّ ما يتولّد منها. (وَمِمَّا لَا يَعْلَمُونَ) أي ومما لم يطلعهم الله تعالى على خصوصياته لعدم قدرتهم على الإحاطة بها، ولما لم يتعلق بذلك شيء ملحٌّ من مصالحهم الدينية والدنيوية وإنما أطلعهم على ذلك بطريق الإجمال. ولو كان لهم به حاجةٌ ملحّة لأعلَمَ به كما أعلَمَ بأحوال الآخرةِ وغيرها مما لم نكن نعلمه (البقاعي 1995 ج 6 ص 261، الزمخشري 19 م 3 ص 322، العمادي 1994 ج 7 ص 167). وإنَّ في الجنّة من النعيم ما لا عين رأت ولا أذن سمعت ولا خطر على قلب بشر. فأعلمنا سبحانه وتعالى بوجوده وإعدادِه ولم يعلمنا به ما هو (فَلَا تَعْلَمُ نَفْسٌ مَا أُخْفِيَ لَهُمْ مِنْ قُرَّةِ أَعْيُنٍ) [السجدة 17].

وفي عصرنا اتّضح معنى الزوجيّة بشكل أوسع حتى شمل الحيوان والنبات، والجماد والمجرّات، فما من ذرّة إلاّ وعنصر الزوجيّة فيها موجود، والآية قالت: (وَمِنْ كُلِّ شَيْءٍ خَلَقْنَا زَوْجَيْنِ) [الذّاريات 49] فكان فيما اكتشفه الإنسان في هذا الموضوع معجزة من معجزات القرآن، ودليلاً على عظم الخالق وقدرته وسعة ملكه وسلطانه (حوّى 19 م 10 ص 5522، العمادي 1994 ج 7 ص 167).

وقوله: (مِمَّا تُنْبِتُ الْأَرْضُ وَمِنْ أَنْفُسِهِمْ وَمِمَّا لَا يَعْلَمُونَ) [يس 36] يُعدّدُ الأصناف لتأكيد العموم ... من غير تقييد. وقوله (وَمِمَّا لَا يَعْلَمُونَ) يُدخِل ما في أقطار السماوات وتخوم الأرضين وهذا دليل على أنه لم يذكر ذلك للتخصيص ... وإنما ذكر الأشياء لتأكيد معنى العموم. وفيه معنى لطيف وهو أنه تعالى إنما ذكر كون الكلّ مخلوقاً لينُـزّه الله عن الشريك (الرّازي 1995 م 13 ج 26 ص 70). وإنَّ الآية (سُبْحَانَ الَّذِي خَلَقَ الْأَزْوَاجَ كُلَّهَا مِمَّا تُنْبِتُ الْأَرْضُ وَمِنْ أَنْفُسِهِمْ وَمِمَّا لَا يَعْلَمُونَ) [يس 36] لتؤكّدُ وحدانية الخالق الّذي أوجد قاعدة التكوين مع اختلاف الأشكال والأحجام والأنواع والأجناس، والخصائص والسّمات ... ومن يدري فربّما كانت هذه قاعدة الكون كلّه حتى الجماد! (قطب 1996 م 5 ص2967). وكذلك هي القاعدة في عالم الذّرة وغيره ممّا يكتشفه الإنسان شيئاً فشيئاً (حوّى 19 م 9 ص 5126). وقد أصبح معلوماً أنّ الذّرة مؤلفة من زوجين مختلفين من الكهرب، سالب وموجب ... كذلك شوهد ألوف من الثنائيات النّجميّة. تتألف من نجمين مرتبطين يشدّ بعضهما بعضاً، ويدوران ... كأنّما يوقعان على نغمة رتيبة (قطب 1996 م 5 ص2967).

إنّ من واجب المسلمين توظيف العلوم من أجل بيان عظمة وإعجاز هذا الكتاب. وأرى أنّ من واجبي بيان الإعجاز الرياضي في القرآن الكريم. وقد منّ اللّه عليّ بنشر أربعة أبحاث في موضوعي الإعجاز والفيزياء الكونيّة في القرآن. يعرض هذا البحث أمثلة لأزواج رياضيّة، ممّا يوضّح بيان إعجاز الآيات الّتي أكّدت أنّ الخلق أزواج. وأسأل اللّه تعالى أن يخدم هذا الجهد موضوع الإعجاز وأن يقيم الحجّة على غير المسلمين.

المطلب الثاني: بعض الأزواج في الرياضيات

الجمع وضدّه الطرح، الضرب وضدّه القسمة، التكامل وضدّه التفاضل، التفاضل نوعان: الكلّي والجزئي، الاشتقاق: العادي والكسري والمعقّد. الاقترانات منها: خطّي وغير خطّي، ومنها المتجانس وغير المتجانس، ومنها متماثل المناحي الاتجاهيّة وغير متماثل المناحي الاتجاهيّة.

المصفوفات (Matrices) وأنواعها:

مصفوفة التفرّد (Singular matrix) محدّدتها صفريّة ليس لها معكوس. بينما المصفوفة الّتي محدّدتها غير صفريّة (Non-singular matrix) لها معكوس (Lipschutz 1968, P. 176, Kahn 1990, P. 63).

المصفوفة المتناظرة (Symmetric matrix) المصفوفة تساوي المقلوب (Lipschutz 1968, P. 65):

مصفوفة التعامد (Orthogonal matrix) مقلوب المصفوفة يساوي معكوسها (Lipschutz 1968, P. 287):

المصفوفة المربّعة (Square matrix) عدد الصفوف يساوي عدد الأعمدة

مصفوفة الوحدة (Identity matrix):

المصفوفة القطريّة (Diagonal matrix) جميع عناصرها غير القطريّة أصفار

مصفوفة مثلّثيّة (Triangular matrix) وهي نوعان (Lipschutz 1968, P.43):

مصفوفة مربعة جميع عناصرها أسفل القطر الرّئيس أصفار ( Upper triangular matrix). مصفوفة مربعة جميع عناصرها فوق القطر الرّئيس أصفار (Lower triangular matrix) . حيث عناصر القطر الرّئيس (main diagonal) هي:

المصفوفة الهيرميتيّة (Kahn. 1990, P. 16, 38) (Hermitian matrix):

Hermitian matrix: real-symmetric, have a complete set of linearly independent eigenvectors even if their eigenvalues coincide. Matrix A is Hermitian if it is equal to its adjoint, i.e. iff

والأزواج عديدة في المجموعات: فمثلاً مجموعة مفتوحة، وأخرى مغلقة، كليّة وجزئيّة، وخالية ... الخ. وإنّ مجموعات الأعداد هي أنواع : الأعداد المعقّدة (Complex)، والحقيقيّة (Real)، والنِّسبيّة (Rational)، والصَّحيحة (Integers)، والطّبيعيّة (Natural).

الفرع الأوّل: أزواج الإقترانات

بعض الإقترانات الرياضيّة واحد – لواحد (One-to-One):

I - if x1 is not equal to x2 then f(x1) is not equal to f(x2). OR,

II - if f(x1) = f(x2) then x1 = x2.

Example 1: The function f (x) = x³ is One-to-One.

وبعض الإقترانات تعدُّدي (ONTO):

A function is called an ONTO function if the range of f is B. In other words, if for each b ∈ B there exists at least one a ∈ A such that.
f(a) = b, then f is an ONTO function

The function f (x) = 3x - 4 (a straight line) is ONTO.

Example 2: State whether the given function is ONTO or not. defined by f(x) = 1 + x ² .

Solution: f(x) = 1 + x ²

Let x = 1

f(1) = 1 + 1 ²

f(1) = 2 ----(equation 1)

Now, let x = -1

f(-1) = 1+ (-1) ²

f(-1) = 2 -----(equation 2)

but 1 ≠ -1

∴ f is not a One-to-One function.

If f is onto then 0 ∈ R

f(x) = 0

1 + x ² = 0

x ² = -1

does not belong to R

∴ f is not an ONTO function

Example 3: The function g (x) = x² - 2 (a parabola) is NOT ONTO. Values less than -2 on the y-axis are never used. In addition, this parabola has y-values that are paired with more than one x-value, such as (3, 7) and (-3, 7). This function will not be One-to-One. ([1])

Description: ontopic2

ويناظره في الحياة البشريّة أنَّ بعض الرّجال له زوجة واحدة، وبعضهم له أكثر من زوجة. كما أنّ قوانين الشّريعة لا تسمح أن يكون للمرأة أكثر من زوج (قرين)، فإنَّ قوانين الرياضيات لا تسمح أن يكون لعنصر المجال (المتغيّر المستقلDomain ) أكثر من صورة في المدى (Range). الاقتران:

هو عبارة عن أزواج مرتّبة في المستوى الديكارتي. وأما الاقتران

فهو معكوس الاقتران السّابق؛ إذا كان الاقتران واحداً – لواحد (One-to-One).

الفرع الثاني: أزواج الاقترانات الدائريّة (الجيبيّة)

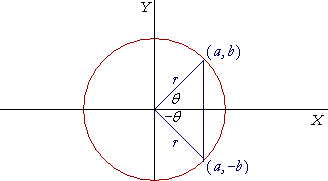
في دائرة الوحدة، يتحدّد المثلث قائم الزاوية بأحد ضلعي القائمة، فيتحدّد تبعاً لذلك الضلع الأخير. إذن الزّوجان هما:

يمكن أن يتولّد من هذين الزّوجين ؛ أي يكتب بدلالتيهما؛ جميع الاقترانات الدائريّة. كما أنّه يمكن الحصول على جيب التمام بدلالة الجيب وبالعكس:

ويناظره في الحياة البشريّة أنّ اللّه تعالى قد خلق الذّكر من الأنثى والأنثى من الذّكر. يقول سبحانه: (هو الّذي خلقكم من نفسٍ واحدة وجعل منها زوجها) [الأعراف 189]. قوله تعالى (هو الّذي خلقكم من نفسٍ واحدة ) قال جمهور المفسّرين: المراد بالنّفس الواحدة آدم. (وجعل منها زوجها) يعني حوّاء (القرطبي م 4 ج 7 ص 214).

جعل الإسلام القوامة للرجل على المرأة. هذا ويتقدّم اقتران جيب التمام المسير على اقتران الجيب بزاوية طور مقدارها تسعين درجة:

The graph of sine and cosine:

(http://commons.wikimedia.org/wiki/File:Sine_cosine_plot.svg)

وإليك بعض تزاوجات الإقترانات الدائريّة (Gradshteyn and Ryzhik 1983 p. 24):

يبيّن الشّكل دائرة الوحدة، ومن تشابه المثلثات يتضح أنّ الطول DE يساوي ظل الزاوية.

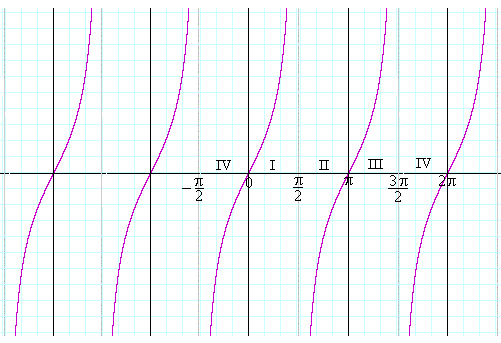
Description: 116

يبيّن الشّكل دوريّة الاقتران

وأما الاقترانات المشتقة فهي:

الفرع الثالث: القطوع الزائديّة

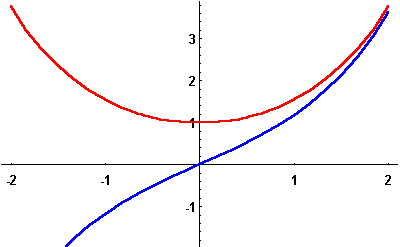
Description: hyper011

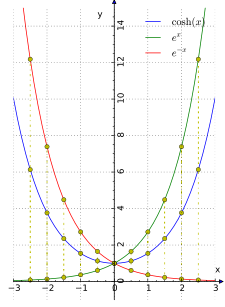
يمثل المنحنى باللون الأحمر الاقتران

وهو even function . وإنه ليعلو المنحنى الأزرق، والذي يمثل الاقتران (odd function):

ويمكننا النظر إلى الإقتران على أنّه يمثل القيمة المتوسطة للإقترانين : (الشكل التالي).

ويمكننا النظر إلى الإقتران على أنّه يمثل نصف الفرق بين الإقترانين : .

Description: (a) cosh(x) is the average of exand e−x

(a) cosh(x) is the average of e^xand e^−x

يبيّن الشكل الآتي جميع الاقترانات الزائديّة:

tanh x	coth x

sech x	csch x

الزّوجان الأساسيّان هما:

ومن هذين الزوجين يمكن أن يتولّد جميع الاقترانات الزائديّة المبيّنة في الشكل السّابق. وفيما يلي بيان لهذه التزاوجات:

ويمكن التزاوج بين الإقترانات الزائديّة و الدائريّة ، وإليك بعض هذه التزاوجات أو الإقترانات (Gradshteyn and Ryzhik 1983 p. 24):

تبيّن العلاقة الأخيرة كيفيّة الحصول على أيّ من الزوجين الأساسيّين من قرينه.

الفرع الرابع: بعض تزاوجات المجموع والفرق

وإليك بعض هذه التزاوجات (Gradshteyn and Ryzhik 1983 p. 24-25)

الفرع الخامس: التزاوجات بين معكوس الاقترانات الدائريّة ومعكوس الاقترانات الزائديّة

معكوس الاقترانات الدائريّة : كما هو مبين في الشكل التالي، فإنّ المراد بمعكوس الاقترانات الدائريّة تعطيه العلاقتان:

وفيما يلي بعض التزاوجات بين معكوس الاقترانات الدائريّة ومعكوس الاقترانات الزائديّة (Gradshteyn and Ryzhik 1983 p. 47) :

الفرع السادس: بعض تزاوجات التكامل - التفاضل الأساسيّة .(Anton et al. 2002)

الفرع السابع: الدّوال الخاصّة (Special functions)

هناك علاقات تكراريّة(Recursion relation-ships) تربط الرّتب المختلفة للدّوال الخاصَّة:

دالّة جاما (Boas 1983, p. 459) ( Gamma function)

For any positive integer $n$ ,

Description: gammaplot

وهناك كذلك دالّة جاما بدلالة متغير مستقل معقّد (complex):

The complex gamma function is defined as:

Where z is a complex number with a positive real component.

كثيرات حدود لجندر ((Boas 1983, p. 490- 491) (Legendre polynomials

هناك علاقات تكراريّة تربط الرّتب المختلفة لكثيرات حدود لجندر ومشتقاتها من الرتبة الأولى:

يمكن كتابة كثيرات حدود لجندر من الرتب العليا بدلالة الزّوجين الأساسيّيين:

الدّالّة المولّدة (Generating function of Legendre polynomials) هي:

يبيّن الشكلان التاليان رسومات لحدود لجندر من النوعين الأوّل والثاني (http://www.efunda.com/math/legendre/legendre.cfm ).

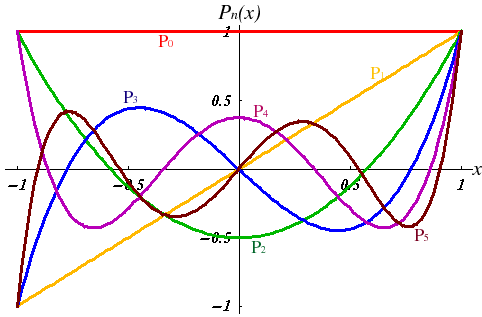
Description: LegendrePPlot

Legendre Polynomial of the First Kind: is even, while is odd. Also

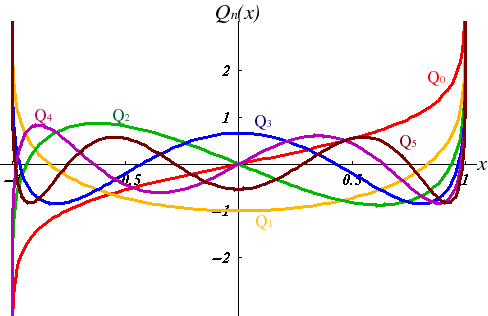
Description: LegendreQPlot

Legendre Polynomial of the Second Kind: is even, while is odd.

هناك علاقات تكراريّة تربط الرّتب المختلفة لدوالّ بسل (Bessel functions) ومشتقاتها من دوالّ الرتبة الأولى (Boas 1983, p. 514) :

يمكن كتابة دوال بسل من الرتب العليا بدلالة الزّوجين :

يبيّن الشكلان التاليان رسومات دوال بسل من النوعين الأوّل والثاني :

(http://www.efunda.com/math/bessel/besselJYPlot.cfm).

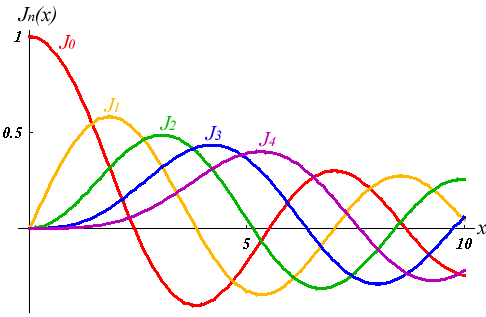
Description: BesselJPlot

Bessel Functions of the First Kind: leads , and has a greater amplitude.

https://www.efunda.com/math/bessel/images/BesselJPlot.gif

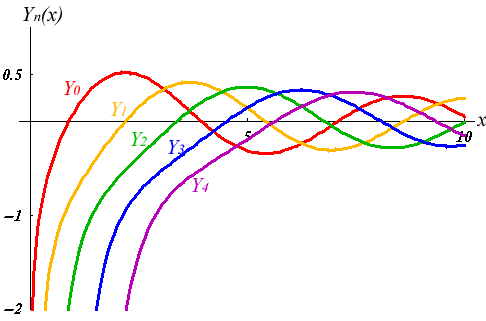
Description: BesselYPlot

Bessel Functions of the Second Kind

هناك علاقات تكراريّة تربط الرّتب المختلفة لكثيرات حدود هيرميت (Hermite polynomials) ومشتقاتها من الرتبة الأولى (Boas 1983, p. 531) :

يمكن كتابة كثيرات حدود هيرميت من الرتب العليا بدلالة الزّوجين الأساسيّين:

الدّالّة المولّدة (Generating function) هي:

يبيّن الشّكل التالي رسوما لحدود هيرميت (http://www.efunda.com/math/Hermite/Hermite.cfm )

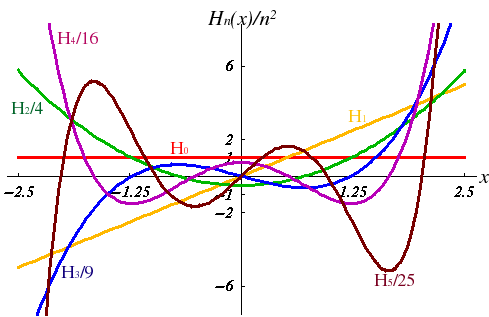
Description: HermiteHPlot

Hermite Polynomial: is even, while is odd.

متعدّدة حدود لاجير (Laguerre polynomials): وتعرّف بالعلاقة التالية:

Description: laguerre

هناك علاقات تكراريّة تربط الرّتب المختلفة لكثيرات حدود لاجير ومشتقّاتها من الرتبة الأولى (Boas 1983, p. 532)

يمكن كتابة كثيرات حدود لاجير من الرتب العليا بدلالة الزّوجين :

الدّالّة المولّدة (Generating function) هي :

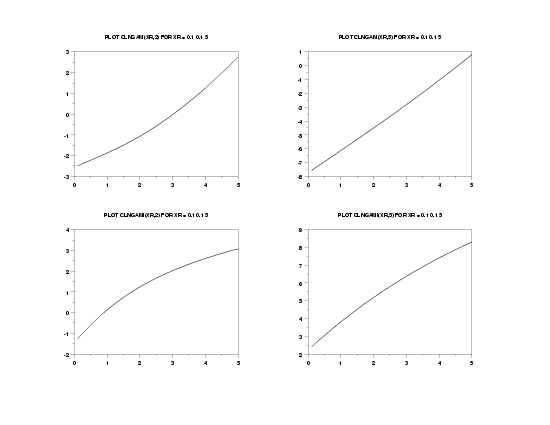
فيما يلي رسما لكثيرات حدود لاجير ([2]):

ومن الأضداد الرياضيّاتية تحويلات لابلاس ومعكوسها (Boyce 1977) .

الفرع الثامن: الانتقالات (Transformations)

وللتفصيل في بعض هذه الجزئيّات ، أنظر في بحث الأزواج الفيزيائيّة الفرع السادس؛ فرع الانتقالات أو التّحوّلات (Transformations):

تدوير نظام محاور الإسناد ومصفوفة التحويل:

Rotation of coordinate system, The Transformation Matrix

تدوير حول المحور x بزاوية a : العلاقات بين مركبات المتجه في النظامين هي:

تدوير حول المحور y بزاوية b : العلاقات بين مركبات المتجه في النظامين هي:

تدوير حول المحور z بزاوية g : العلاقات بين مركبات المتجه في النظامين هي:

تدوير حول المحاور الثلاثة: يمكن كتابة المتجه بدلالة متجهات الوحدة الأساسيّة (unit basis vectors) على النحو التالي:

العلاقة بين المركبات في النظامين تعطى بدلالة مصفوفة الانتقال (Fowles Cassiday p. 22 ):

انتقالات لورنتز (Lorentz Transformation)وانتقالات جاليلو (Galilian Transformation) (الشكل الآتي):

$Description: \includegraphics[width=0.7\textwidth]{ref_frames.eps}$

Figure 1: Reference frame S' moves with velocity (in the x direction) relative to reference frame S.

انتقالات لورنتز (Lorentz Transformation):

دوالّ الموقع والزمن في الإطار المتحرّك هي:

دوالّ الموقع والزمن في الإطار السّاكن هي:

تصبح هذه العلاقات على صورة انتقال جاليلو (Galilian Transformation)في حالة كون السرعة

- تحوّلات فورير (Fourier Transforms) (Boas, 1983, p. 648).

A Fourier transform is nothing more than a change of basis; it simply allows you to represent the same object in a different way.

The far-field scattering pattern for light is (under certain conditions) the Fourier transform of the aperture. In crystallography and such, the scattering pattern (Laue pattern) is the Fourier transform of the charge distribution within a unit cell.

Fourier transforms are used a lot in optics. It has a very physical application- the optical field at a focal plane is the Fourier transform of the optical field at the opposite pupil plane.

Electrical signal processing is another real-world use: the equalizer on a stereo, or windows media player. Guitar effects can work via manipulating the frequency content (http://www.physicsforums.com/showthread.php?t=217204).

يمكن كتابة الاقتران الدّوري f(x) بدلالة متسلسلة فورير على الصورة:

دورة الاقتران الدّوري f(x) هي 2l ، وتردّدات حدود متسلسلة فورير هي n/2l. في حالة التردّدات المستمرّة ، فإنّ انتقالات فورير هي:

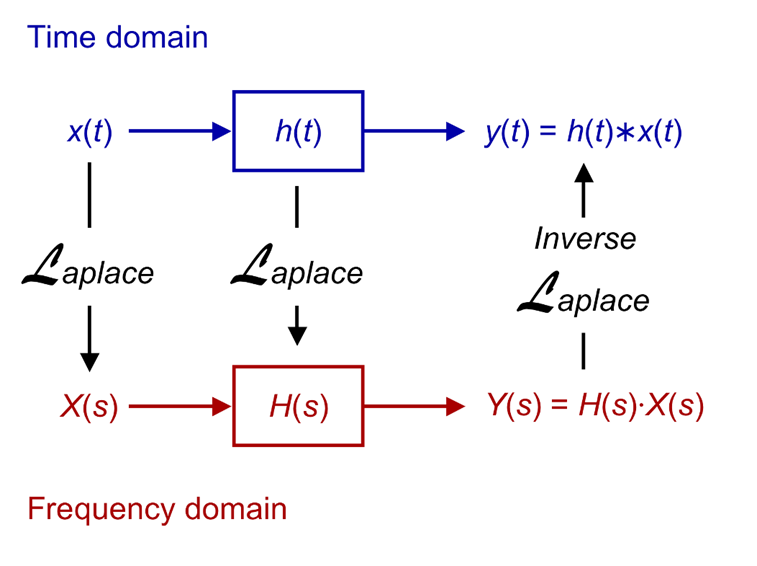
- تحولات لابلاس (Laplace Transforms) (Boas, 1983, p. 639).

يعرّف L(f) (تحويل لابلاس للإقتران f(t)) بالعلاقة التالية:

; .

the Laplace transform is one of the best known and most widely used integral transforms. It is commonly used to produce an easily solvable algebraic equation from an ordinary differential equation. The Laplace transform is often interpreted as a transformation from the time-domain, in which inputs and outputs are functions of time, to the frequency-domain, where the same inputs and outputs are functions of complex angular frequency, or radians per unit time. Laplace transform provides an alternative functional description that often simplifies the process of analyzing the behavior of the system (http://en.wikipedia.org/wiki/Laplace_transform#Examples:__How_to_apply_the_properties_and_theorems).

the inverse Laplace transform, is given by the formula:

where the integration is done along the vertical line $Re (p) = γ$ in the complex plane such that $γ$ is greater than the real part of all singularities of F( $p$ ).

Description: LTI .

المراجع والمصادر

المصادر

القرآن الكريم

المراجع العربيّة:

1) ابن كثير القرشي الدمشقي، عمادالدين أبي الفداء (ت 774 هـ)، تفسير القرآن العظيم، دار الفيحاء (دمشق الطبعة الأولى 1414 هـ - 1994 م)، أربع مجلدات.

2) ابن منظور، (630-711 هـ)، لسان العرب، مؤسّسة التاريخ العربي- بيروت، الطبعة الثالثة (1413 هج- 1993 م)، ج 6 ، ص 107-109.

3) أبو حيان الأندلسي الغرناطي، محمد بن يوسف ( 654-758 هـ)، البحر المحيط في التفسير، دار الفكر (بيروت-لبنان 1412 هـ - 1992 م)، عشرة أجزاء.

4) البقاعي، برهان الدين (ت 885 هـ)، نظم الدرر في تناسب الآيات والسور، دار الكتب العلمية (بيروت-لبنان 1415 هـ - 1995 م)، ثمانية أجزاء .

5) حوّى، سعيد ، الأساس في التفسير، دار السّلام (مصر 1409 هـ - 1989 م). م 8 ص 4650.

6) الخطيب، عبدالكريم ، التفسير القرآني للقرآن، دار الفكر (القاهرة 1386 هـ - 1967 م)، ثلاثون جزءاً م 12، ص 931.

7) الرّازي، فخر الدين (544-604 هـ) ، التفسير الكبير ومفاتيح الغيب، دار الفكر (بيروت-لبنان 1415 هـ - 1995 م)، سبعة عشر مجلداً. م 14 جزء 28 ص 228.

8) الزمخشري، أبو القاسم جار اللّه محمود بن عمر (467-538 هـ) ، الكشاف عن حقائق التّـزيل وعيون الأقاويل في وجوه التّأويل، دار الفكر (بيروت-لبنان 1397 هـ - 1977 م)، أربع مجلّدات.

9) السيوطي، عبدالرحمن جلال الدين، الدّر المنثور في التفسير المأثور (ت 911 هـ)، دار الفكر (بيروت-لبنان الطبعة الثانية 1414 هـ - 1993 م)، ثمانية أجزاء . م7، ص 55.

10) الطبري، تفسير الطبري، (دار الفكر 1415 هـ - 1995 م)، م 13 جزء 25 ص 68.

11) العمادي، أبي السعود محمد بن محمد (951 هجري)، تفسير أبي السعود إرشاد العقل السليم إلى مزايا القرآن الكريم، دار إحياء التراث العربي (بيروت الطبعة الرابعة 1414 هج-1994 م)، تسعة أجزاء.

12) القرطبي، أبي عبدالله محمد بن أحمد (ت 671 هجري)، الجامع لأحكام القرآن، دار الكتب العلمية (بيروت-لبنان الطبعة الخامسة 1417 هـ - 1996 م)، واحد وعشرون مجلّدا .

13) قطب، سيّد، ظلال القرآن، الطبعة الشرعيّة الخامسة والعشرون (دار الشروق القاهرة: 1417 هـ - 1996 م). م 5، ص 2967.

المراجع الأجنبيّة:

14) Anton, H., Bivens, I., Davis, S., Calculus, 7^th. Ed. 2002, John Wiley and Sons, New York, P. 196, 463, 201, 513.

15) Boas, Mary L., Mathematical methods in the physical sciences, second ed. 1983, John Wiley and Sons, Singapore, Page 459.

16) Boyce, W. E. And DiPrima, R. C., Elementary differential equations and boundary value problems, John Wiley and sons, Newyork, 3rd. Ed. 1977, page 236.

17) Gradshteyn, I. S. and Ryzhik, I. M., Table of Integrals, Series, and Products, Academic press, New York, 4^th. Printing, 1983, P.24.

18) Kahn, Peter B., Mathematical methods for scientists and engineers. 1990, John Wiley, New York, P. 63.

19) Lipschutz, Seymour, Linear Algebra. 1968, Schaum McGraw-Hill, New York, P. 176.