(http://hyperphysics.phy-astr.gsu.edu/hbase/nucene/nucbin.html)
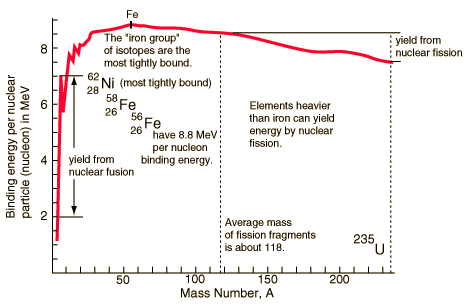
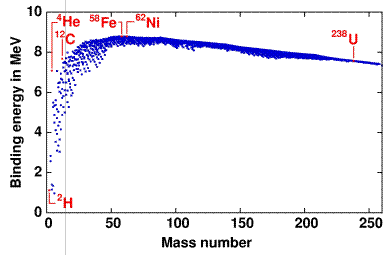
At the
peak of binding energy, nickel-62
is the most tightly-bound nucleus, followed by iron-58 and iron-56. [1] (This is the basic
reason why iron and nickel are very common metals in planetary cores, since
they are produced abundantly as end products in supernovae
and in the final stages of silicon burning in Stars). Iron-56 is more common
than nickel isotopes because its unstable progenitor nickel-56 is copiously made by
staged build-up of 14 helium nuclei inside supernovas, and it then decays to iron-56 within a few weeks. (http://wapedia.mobi/en/Binding_energy?t=3.)
The Most Tightly Bound Nuclei
The most tightly bound of the nuclei is 62Ni, a case made convincingly by M. P. Fewell in an article in the American Journal of Physics. Though the championship of nuclear binding energy is often attributed to 56Fe, it actually comes in a close third. The four most tightly bound nuclides are listed in the table below with a tabulation of the binding energy B divided by the mass number A. The curve adapted from Fewell shows those nuclides that are close to the peak.
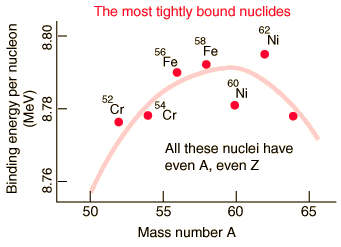
Data from Wapstra and Bos. |
(http://hyperphysics.phy-astr.gsu.edu/hbase/nucene/nucbin2.html#c2)
The absolute nuclear binding energy is the hypothetical energy release if a given nuclide were synthesized from Z separate hydrogen atoms and N (equal to A − Z) separate neutrons. An example is the calculation giving the absolute binding energy of the stablest of all nuclei, iron-56:
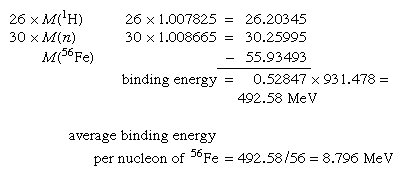
(http://www.aei.mpg.de/einsteinOnline/en/spotlights/binding_energy/index.html)
(http://www.vikdhillon.staff.shef.ac.uk/teaching/phy213/phy213_fusion1.html)
1. If I understand your question correctly, you wonder why hydrogen (H-1)
can have a binding energy with only a single proton?
Nuclear binding energy arises from the attraction of the Strong nuclear force
between nucleons (protons and neutrons). In a nucleus, this binding energy is
stronger than the electromagnetic repulsion force that would exist if the
nucleus contained more than 1 proton. The more nucleons, the stronger the total
strong force is in the nucleus. However, as nucleons are added, the size of the
nucleus gets bigger, so the ones near the outside of the nucleus are not as
tightly bound as the ones near the middle of the nucleus. The binding energy
per nucleon, because of the variation of the strong force with the distance,
increases until the nucleus gets too big and the binding energy per nucleon
starts decreasing again. This binding energy per
nucleon achieves a maximum around A = 56, and the only stable isotope with that
A number is iron-56. So the way fusion works in a star is that the force of gravity is strong
enough to get the nucleons close enough together so that the EM repulsion is
overcome, causing fusion. So, looking at hydrogen, once its nucleus gets close
enough to fuse with more nucleons (say in another hydrogen)
energy is released.
2. Think of excess binding energy like a ball on a staircase, where the ground
state (the state where the ball has the least energy) is the ball at the bottom
of the stairs. If the ball is somewhere on one of the steps, at some point the
ball rolls down the stairs. The potential energy of the ball at the higher step
is released as sound energy (assuming no other mechanism for energy release
existed). In a nucleus, the excited states of the nucleus are the steps of the
staircase, and the gamma photon that is released from the nucleus is analagous
to teh sound energy that is released.
Uh, firstly, hydrogen normally does not contain any neutron (just the one
nucleon, a proton).
The most "stable" atom is of Iron. This is to
say, the lowest energy state for a collection of nucleons is a state in which
they are grouped into iron nuclei.
If you try to concentrate a larger number of nucleons into the nucleus, the
basic problem (simplified, no doubt) is that the (long range) electrostatic
repulsions between the protons will be more strained, increasing the amount of
potential energy stored (on a per-nucleon basis). As nuclei gets larger, you
can imagine it stretching further than the strings of "glue" holding
it together (the short range "strong force") can reach. So, with
heavy atoms (like Uranium), you will release a lot of electrostatic energy if
you let the atom split in two (and this won't be prevented by the strong force,
which hardly reaches across such large nuclei).
But if you try to break Iron nuclei in two, even though the electrostatic
repulsion will help you, you'll need to provide even more energy. This is
because the nucleus is small enough for the strong force to "hold both
ends together", you need extra energy to overcome
this force. Conversely, if you take two little deuterium nuclei, and hold them
near together (by supplying a little bit of energy to get past the long range
electrostatic repulsion, and bring them just into range of the strong force)
then they'll tug so tightly toward each other that you can obtain lots of
energy letting them fuse the rest of the way together.
It seems like you're confused by thinking to much of "binding energy"
as something "contained" in atoms.
(http://www.physicsforums.com/archive/index.php/t-168832.html)
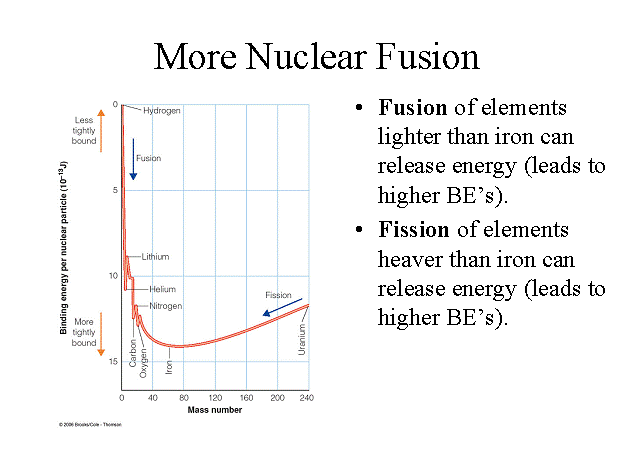
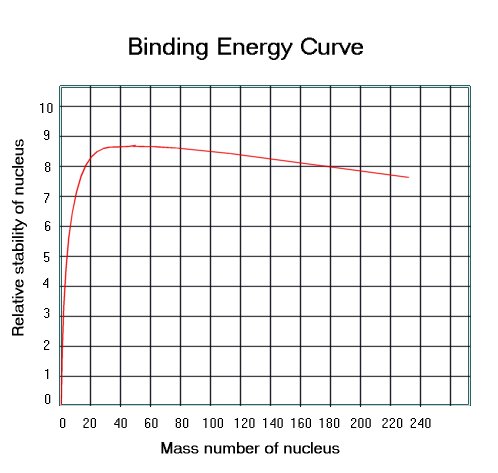
Remember how I said that the greater the binding energy
per nucleon of an atom, the greater it's stability? Well, above is a
graph of the relative binding energy per nucleon vs. mass number (total number
of nucleons composing an atom). Notice that the nuclei of the light elements
are generally less stable than the heavier nuclei up to those with a mass
number around 56. The nuclei of the heaviest elements are less stable than the
nuclei that have a mass number of around 56. From this, you can see that the
nuclei around iron are the most stable. This information implies two methods
towards the converting of mass into useful amounts of energy: fusion and
fission.
(http://library.thinkquest.org/17940/texts/binding_energy/binding_energy.html)
(file:///C:/Documents%20and%20Settings/Administrator/Local%20Settings/Temporary%20Internet%20Files/Content.IE5/ZWU8D2KZ/278,23,Slide 23)
(file:///C:/Documents%20and%20Settings/Administrator/Local%20Settings/Temporary%20Internet%20Files/Content.IE5/ZWU8D2KZ/278,23,Slide 23)
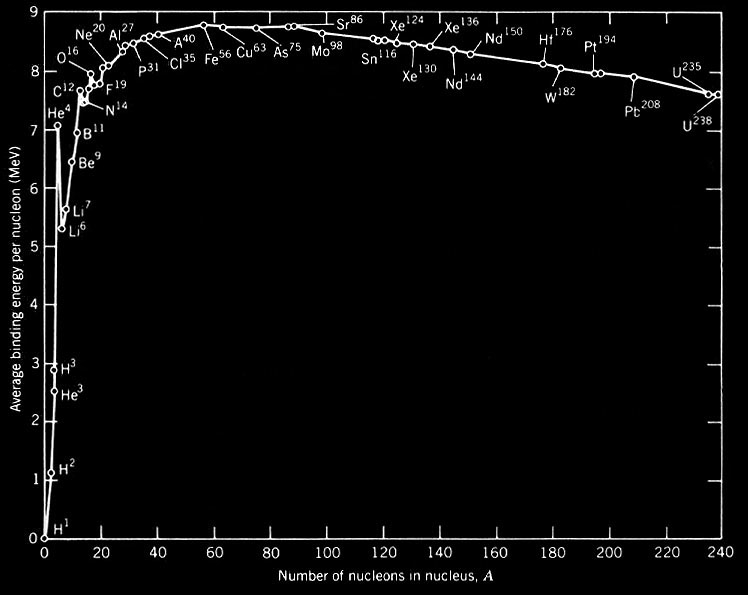
The isotope with the
shortest average internal nuclear length, and hence the weakest binding energy
per nucleon is Hydrogen 5. The isotopes with the longest internal nuclear
lengths are Nickel 62, Iron 56, and Iron 58, and thus have the strongest
binding energy per nucleon.
The shells of the nucleus fill according to 2, 8, 20, 28, 50, 84, 126. Iron 58 appears to be a point where all four
inner shells are completely full (2+8+20+28=58). Iron 56 appears to be a
point where the second, third and fourth shells are completely full
(8+20+28=56). Nickel 62 appears to be a situation where all four of the
inner shells are full and an alpha particle (helium nucleus) may be formed in
the 5th shell. (2+8+20+28+4=62). From these observations it may be
correct to say that the internal nuclear length equation is dependent on the
shell structure and fill pattern of the nucleus.
(http://www.16pi2.com/internal_nuclear_length.htm)
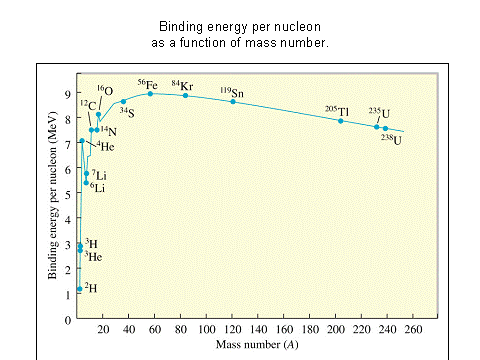
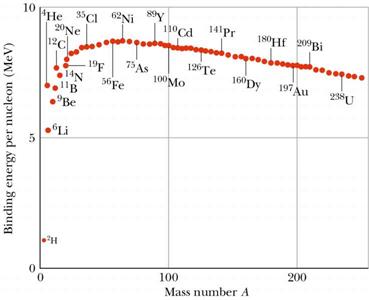
From this graph we can see the following:
· The vast majority of nuclides have a binding energy of 8 MeV per nucleon.
· Helium has a particularly high value of binding energy per nucleon, much higher than the light isotopes of hydrogen.
· There is a trend for
nuclides of nucleon numbers in multiples of 4 to be particularly stable (i.e.
have a high binding energy).
· Fe is the most stable
nuclide.
· The largest nuclides tend to be less stable, with slightly lower binding energies per nucleon.
Iron has the highest binding
energy per nucleon so is the most stable nucleus. If we look at large nuclei (greater than
iron), we find that the further to the right (greater nucleon number) the less
stable the nuclei. This is because the
binding energy per nucleon is getting less.
The explanation for this observation lies in that the strong nuclear
force that binds the nucleus together has a very limited range, and there is a
limit to the number of nucleons that can be crammed into a particular space.
(http://www.antonine-education.co.uk/physics_a2/module_4/Topic_11/topic_11.htm)
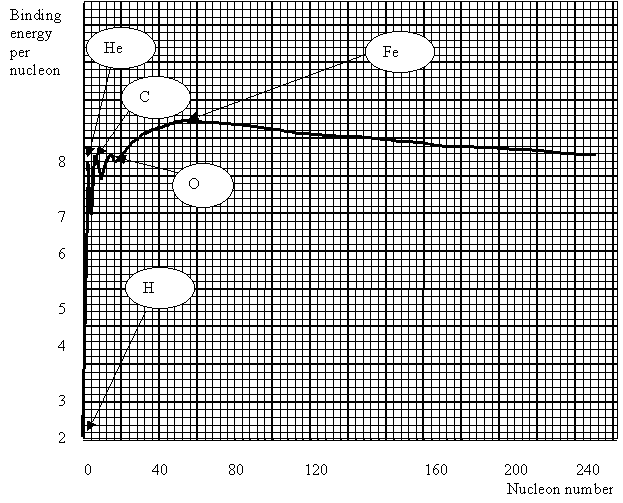
Notice that iron has the highest binding energy per
nucleon and that this binding energy drops off as the mass of atoms increases
after iron. Recall that stars can only fuse atoms together up to iron, which is
the most stable nucleus. Heavy atoms such as uranium have relatively low
binding energies per nucleon and if they split apart the binding energy of
their daughter atoms is actually higher. The difference in energy shows up as
heat, which is how we get power out of the fission of uranium.
file:///H:/binding%20energy/Quantum%20physics%20of%20matter%20p133.htm#PPA131,M1
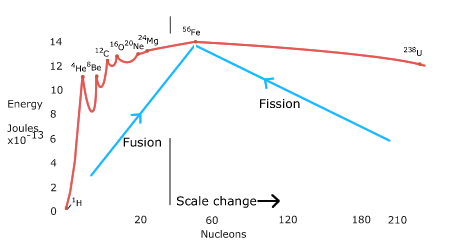
iron peak nuclei
This curve indicates how stable atomic
nuclei are; the higher the curve the more stable the nucleus. Notice the characteristic
shape, with a peak near A=60. These nuclei (which are near iron in the periodic
table and are called the iron peak nuclei) are the most stable in the
Universe. The shape of this curve suggests two possibilites
for converting significant amounts of mass into energy. (http://csep10.phys.utk.edu/astr162/lect/energy/bindingE.html)
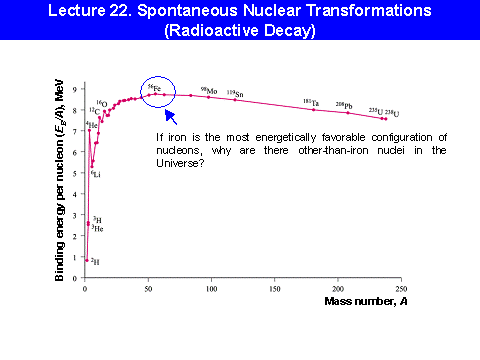
(http://www.physics.rutgers.edu/ugrad/313/Lecture%2022%20Nuclear%20Transformations.ppt)
How does the average binding energy per nucleon change as Z increases? We
find that the average binding energy per nucleon first increases up to iron-56, 
,
then decreases gradually as shown:
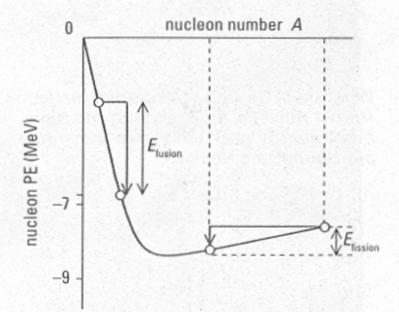
The curve shows that nucleons can fall deeper into the nuclear ``well''
in two circumstances:
If
a nucleus to the right of breaks into smaller pieces, the nucleons
inside the pieces are deeper inside the ``well'' than they had been in the
original nucleus. - fission
If
two nuclei to the left of combine
into a nucleus smaller than ,
the nucleons inside will find themselves deeper inside the ``well.'' - fusion
(http://www.physics.ohio-state.edu/~kagan/phy367/Lectures/P367_lec_14.html)
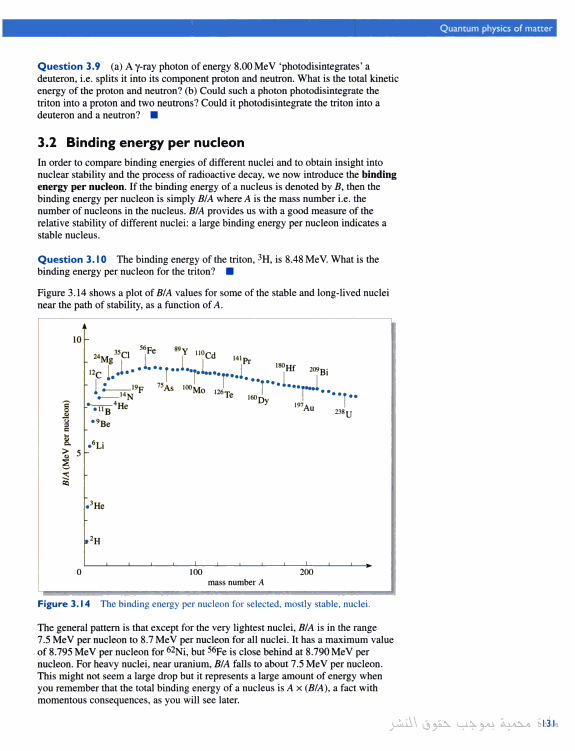
The nuclides of intermediate
mass number have the largest values for the binding energy per nucleon and the
most stable is 
has a value 8.8 MeV it’s the most stable since it need the most energy
to disintegrate.
The smaller values of binding energy
per nucleon for higher and lower mass numbers imply that potential source of
nuclear energy.
The figures show that nuclides with low mass numbers can produce energy by fusion, when two light nuclei have fused to produce a heavier nucleus.
In contrast heavier nuclides (i.e. higher mass numbers) can produce energy by fission (disintegration) into their nuclei into two lighter nuclei.
In both cases, nuclei are produced having great binding energy per nucleon and therefore
1. more
stable nuclei
2
there is consequently a mass transfer during their formation
(http://www.mona.uwi.edu/physics/courses/p04b/documents/Atomic-Radio.doc)
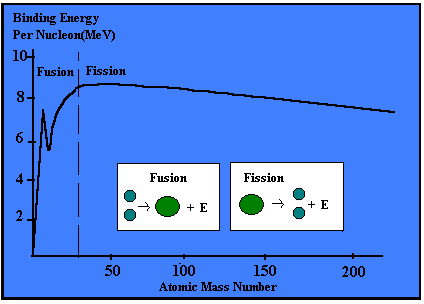
BINDING ENERGY CURVE
In heavier stars the
temperature is higher. In stars of about 10 solar masses, the iron isotope 56Fe
is reached. This is the heaviest nucleus
that can be formed in the core of stars by nuclear fusion.
(http://www.egglescliffe.org.uk/physics/particles/sun/sun.html)
Nuclear fusion
sequence and the alpha process
After
high-mass stars have nothing but sulfur and silicon in their cores, they
further contract until their cores reach in the range of 2.7–3.5 GK; silicon
burning starts at this point. Silicon burning entails the alpha process
which creates new elements by adding the equivalent of one helium nucleus (two
protons plus two neutrons) per step
Type
II supernovae mainly synthesize oxygen and the alpha-elements (Ne, Mg, Si, S,
Ar, Ca and Ti) while Type Ia supernovae produce elements of the iron peak (V, Cr, Mn, Fe, Co and Ni).
The
entire silicon-burning sequence lasts about one day and stops when nickel–56
has been produced. Nickel–56 (which has 28 protons) has a half-life of
6.02 days and decays via beta radiation (in this case, "beta-plus"
decay, which is the emission of a positron) to cobalt–56 (27
protons), which in turn has a half-life of 77.3 days as it decays to iron–56
(26 protons). However, only minutes are available for the nickel–56 to decay
within the core of a massive star. At the end of the day-long silicon-burning
sequence, the star can no longer release energy via nuclear fusion because a
nucleus with 56 nucleons has the lowest mass per nucleon (proton
and neutron) of all the elements in the alpha process sequence.
In stars, rapid nucleosynthesis proceeds by
adding helium nuclei (alpha particles) to heavier nuclei. Although nuclei with
58 and 62 nucleons have the very lowest binding energy, fusing a helium nucleus
into nickel–56 (14 alphas) to produce the next element — zinc–60 (15 alphas) —
actually requires energy in its production rather than releases any.
Accordingly, nickel–56 is the last fusion product produced in the core of a
high-mass star. Decay of nickel-56 explains the large amount of iron-56 seen in
metallic meteorites and the cores of rocky planets
(http://en.wikipedia.org/wiki/Silicon_burning_process)
In stars of about 10 solar
masses, the iron isotope 56Fe is reached. This is the heaviest nucleus that can be
formed in the core of stars by nuclear fusion.
The
star has run out of nuclear fuel and within minutes begins to contract. The
potential energy of gravitational contraction heats the interior to 5 GK
and this opposes and delays the contraction. However,
since no additional heat energy can be generated via new fusion reactions, the
contraction rapidly accelerates into a collapse lasting only a few seconds. The
central portion of the star gets crushed into either a neutron
star or, if the star is massive enough, a black hole.
The outer layers of the star are blown off in an explosion known as a Type II
supernova
that lasts days to months. The supernova explosion releases a large burst of
neutrons, which synthesizes in about one second roughly half the elements
heavier than iron, via a rapid neutron-capture mechanism.
Multiwavelength X-ray, infrared, and optical
compilation image of Kepler's Supernova
Remnant, SN
1604. (Chandra X-ray Observatory)
(http://en.wikipedia.org/wiki/File:Keplers_supernova.jpg)
(http://en.wikipedia.org/wiki/File:Binding_energy_curve_-_common_isotopes.svg)
